Методы линеаризации нелинейностей и нелинейных систем
Основные положения
Поскольку для нелинейных систем автоматического управления не существует общей теории, то естественно стремление использовать математический аппарат ЛСАУ для исследования моделей НСАУ. Для этого должен быть выполнен корректный переход от НСАУ к ЛСАУ, что достигается с помощью линеаризации. Применяют четыреосновных метода линеаризации нелинейностей и нелинейных систем.
1. Линеаризация статических нелинейностей касательными.
2. Линеаризация статических нелинейностей секущими.
3. Гармоническая линеаризация статических и динамических нелинейностей.
4. Статистическая линеаризация статических и динамических нелинейностей.
Каждый метод линеаризации нелинейностей предусматривает специфичное решение всех остальных проблем теории управления, то есть проблем устойчивости, анализа и синтеза НСАУ.
Линеаризация касательными
Пусть
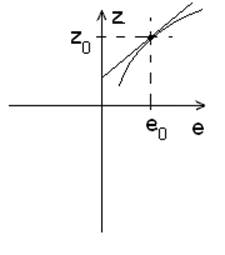
для статической нелинейности аналитически, таблично или графически задана функция F(e). Тогда на этой кривой выбирается рабочая точка
с координатами ![]() . Через рабочую точку проводится
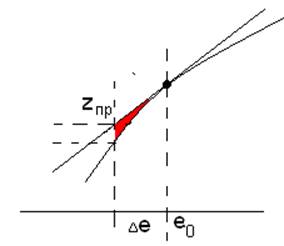
касательная к кривой и определяются отклонения Δe и
ΔΖ, которые можно допустить, заменяя
кривую F(e) прямой (касательной).
. Через рабочую точку проводится
касательная к кривой и определяются отклонения Δe и
ΔΖ, которые можно допустить, заменяя
кривую F(e) прямой (касательной).
![]() - уравнение касательной,
- уравнение касательной, ![]() - коэффициент передачи
безинерционного линейного звена, пропорциональный тангенсу угла наклона касательной
к оси абсцисс.
- коэффициент передачи
безинерционного линейного звена, пропорциональный тангенсу угла наклона касательной
к оси абсцисс.
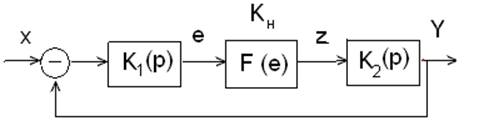
Теперь НСАУ, структура которой изображена, заменяется линейной системой. x, eo, x1, zo,Y - координаты рабочих точек всех элементов САУ.
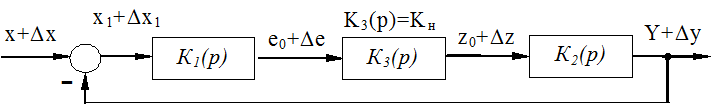
Примечание
1
При изучении линейных САУ такие понятия как "рабочая точка" и её
координаты не учитывались. Почему? Да потому, что поведение САУ рассматривалось
при постоянных параметрах всех её блоков и постоянных начальных отклоненияхкоординат Δx, Δ eo, Δx1, Δzo, ΔY и
"нулевых начальных условиях". Последнее означает, что при t = 0 все
производные перечисленных выше отклонений тоже равны нулю. Тогда и только тогда
справедлив весь математический аппарат теории линейных САУ, опирающийся на
описание их моделей по принципу "вход - выход" в виде: ![]() . Потом как-то "подзабывают",
что
. Потом как-то "подзабывают",
что ![]() и
и ![]() это "малюсенькие" величины по
отношению к постоянным Y и x. Величиной последних даже не интересуются,
поскольку они не влияют ни на устойчивость, ни на качество динамических режимов
моделей ЛСАУ.
это "малюсенькие" величины по
отношению к постоянным Y и x. Величиной последних даже не интересуются,
поскольку они не влияют ни на устойчивость, ни на качество динамических режимов
моделей ЛСАУ.
Иное дело нелинейные системы! Вообразим (почти правдоподобно), что изображенная выше структура представляет систему управления двигателем автомобиля. Скорость движения его колес "Y", а "zо", "x1" и "eо" какие - то воздействия (кинематические, механические, энергетические и другие), которые передают нажатие ногой на педаль "x" задающее воздействие для плавного изменения скорости движения Y. Все прекрасно при большой скорости движения Y, (следовательно, и при больших значениях всех других сигналов "zо", "x1" и "eо"). Машина идет плавно, шины приятно шуршат по асфальту. Но вот автомобиль подъехал к повороту. Водитель привычно сбавляет скорость Y (уменьшая х). Что же творится с машиной: она "фыркает, дергается то вперед то назад, плохо слушается руля? Причиной такого поведения является то, что "рабочая точка" изменилась. При большой скорости Y система работала с большими воздействиями "zо", "x1" и "eо". Теперь "zо", и "eо" стали существенно меньше. В этой новой "рабочей точке" касательная к кривой резко увеличила угол наклона. Следовательно, в прямом канале нелинейной САУ существенно увеличился коэффициент передачи. Переходный процесс стал колебательным, сильно возросли динамические нагрузки. Система теряет устойчивость, и двигателю просто не хватает энергетического ресурса для выполнения неразумных требований.
Рассмотрим более подробно проблему выбора рабочей точки. Пусть НСАУ представлена схемой:
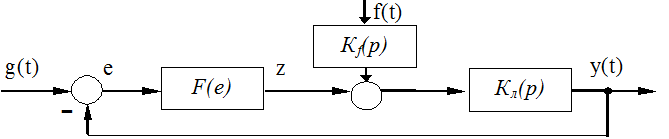
На схеме
обозначены сигнал управления g(t), статическая нелинейность F(e), возмущение
f(t) и операторные функции ЛЧ по возмущению Kf(p) и управлению Kл(р).
Тогда можно записать: ![]() .
.
Эта
формула справедлива для любого момента времени t. Рассмотрим установившееся
движение, которому соответствует «рабочая точка» с координатами ![]() . Тогда, при t → ∞,
получим
. Тогда, при t → ∞,
получим ![]() . Следовательно, для
. Следовательно, для ![]() можно записать выражение:
можно записать выражение:
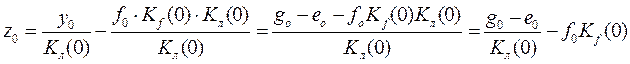 .
.
Полученное уравнение есть прямая линия ![]() . Обозначим в полученной выше формуле
. Обозначим в полученной выше формуле ![]() .
Тогда
.
Тогда
1. при ![]() получаем
точку пересечения прямой оси ординат:
получаем
точку пересечения прямой оси ординат:
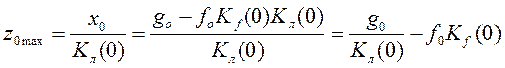 .
.
2) при ![]() получаем
точку пересечения прямой оси абсцисс:
получаем
точку пересечения прямой оси абсцисс:
![]() .
.
Пересечение полученной прямой с кривой ![]() и дает искомую рабочую точку:
и дает искомую рабочую точку:
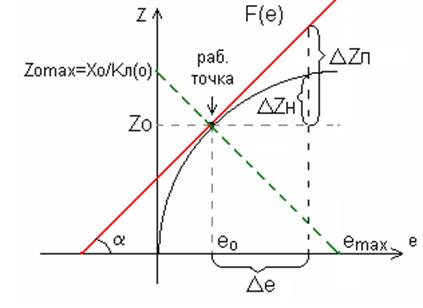
Итак, выбранная «рабочая точка» НСАУ с координатами ![]() и
и ![]() нелинейности F(e) не является
независимой функцией. В замкнутой системе она зависит от второго воздействия
нелинейности F(e) не является
независимой функцией. В замкнутой системе она зависит от второго воздействия ![]() и параметров ЛЧ Кл(0)и Кf(0). Это отражено
в полученной выше формуле.
и параметров ЛЧ Кл(0)и Кf(0). Это отражено
в полученной выше формуле.
Используя метод "линеаризации нелинейности касательными", очень важно определить какие же конкретно можно брать отклонения ∆e и ∆z от рабочей точки? В российской, да и в иностранной литературе нет прямого ответа на этот простой, но очень важный для инженеров-практиков вопрос. Уклончиво рекомендуют "несколько процентов", "до 10%" и так далее.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.