Положение точек М1, Р1, L1 на его сторонах будет задаваться теми же отношениями k1 , k2 , k3 . Площадь нового ∆M1P1L1 будет составлять конкретную долю от площади ∆А1В1С1 независимо от того, на какой из сторон выбрана точка М1 . Для правильного треугольника это аффинное свойство очевидно, а при обратном аффинном преобразовании оно будет «передано» исходному ∆АВС. Ч.т.д.
Вывод. Применение аффинных преобразований уместно в тех задачах планиметрии, которые являются «аффинными», то есть в текстах условий содержат только аффинные понятия и свойства. Идея решения – в замене исходной фигуры на ей аффинно-эквивалентную, более удобную для рассуждений.
§ 3.5. Аффинные задачи на школьном факультативе.
Можно решать аффинные задачи и не зная всех подробностей §§3.1-3.4. Можно даже не употреблять терминов «аффинный», «простое отношение трех точек», и других, не знакомых школьнику. Достаточно хорошо повторить свойства параллельных проекций (стр. 52), начиная с рис.48 и включая перечисленные после него утверждения 1)-4). Итак, полагаем, что школьники освоили доказательство двух теорем.
Теорема 1. При параллельном проектировании образом точки С1, делящей отрезок А1В1 в заданном отношении, будет точка С2, делящая отрезок А2В2 в том же отношении (рис.63).
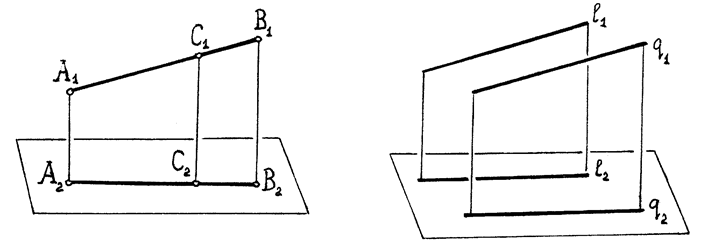
Рис. 63 Рис.64
Теорема 2. Параллельные прямые l1║q1 проектируются в тоже параллельные l2║q2 (рис.64).
Примечание. В противном случае у точки пересечения образов l2 и q2 должен был быть прообраз, что противоречит параллельности l1║q1. Это рассуждение уместно только на основе взаимно-однозначности параллельной проекции (чего нет, например, при центральной).
Приведем еще несколько теорем, позволяющих в результате решать аффинные задачи «методом преобразований». Суть метода, как мы видели в §3.4, в возможности переносить рассуждения с заданного треугольника на более «удобный» (например, равносторонний), либо с заданного параллелограмма – на квадрат, причем гарантировать сохранение аффинных свойств (включая отношение площадей) фигур. Обоснование такой возможности для школьника можно предложить в виде следующих теорем.
Теорема 3. Для любого заданного треугольника АВС существует способ его параллельного проектирования в треугольник требуемой формы (например, в равносторонний).
Доказательство. Проведем через сторону АС произвольную плоскость ω , не содержащую треугольник (рис.65). На стороне АС в плоскости ω построим ∆АСВ1 нужной формы (откладывая при вершинах А и С требуемые углы и пересекая лучи в В1). Прямая l , проведенная через В и В1, задаст направление, по которому ∆АВС спроектируется на плоскость ω в треугольник нужной формы. Ч.т.д.
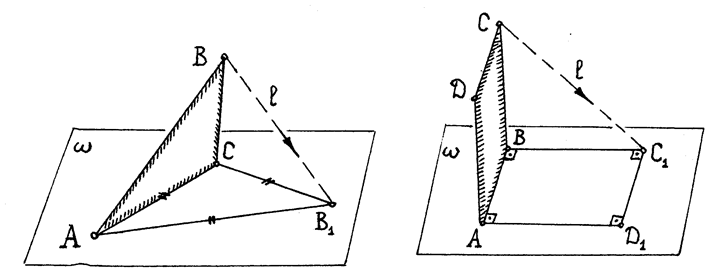
Рис.65 Рис.66
Теорема 4. Для любого заданного параллелограмма АВСD существует способ его параллельного проектирования в квадрат.
Доказательство аналогично предыдущему (рис.66).
Теорема 5. На любой параллельной проекции сохраняется исходное отношение площадей фигур (рис.67).
|
Рис.67 |
Доказательство. При вычислении площади на фигуру накладывают квадратную палетку, проекцией которой будет сетка из параллело- граммов. Количество ячеек, охва-ченных фигурами повторится на проекции независимо от того, как будут (в пределе) измельчать сеть. |
Доказав с учениками перечисленные пять теорем, можно приступать к решению аффинных задач методом «вспомогательной проекции».
Например, в задачах 1, 2 (§3.4) доказательство можно начинать словами: «Согласно теореме 3, существует параллельное проектирова-ние (на некоторую плоскость ω), при котором образом заданного треугольника станет равносторонний треугольник…» Далее логика рассуждений повторяется с формальной заменой термина «аффинное преобразование» на «параллельное проектирование». Этим методом решается любая из приводимых в упражнении 4 (§3.6) задач.
§ 3.6. Задания для самостоятельной работы.
Предлагаемые ниже упражнения рассчитаны на самостоятельное выполнение (по вариантам).
Упражнение 1. Изобразить на числовой оси точки Т, О, К, заданные своими координатами (таблица 6). Перебирая всевозможные сочетания (КОТ), (КТО), и т.д., найти среди простых отношений трех точек наибольшее число и наименьшее.
Упражнение 2. Задать на чертеже некоторое преобразование родства, изобразив ось g и пару (произвольно) соответственных точек В1 и В2. Построить при родстве образ произвольного квадрата, стороны которого не параллельны оси родства.
Упражнение 3. Аффинное преобразование плоскости отображает ∆М1L1P1 в ∆М2L2P2 (координаты х, у всех вершин треугольников заданы в таблице 6). Изобразить треугольники, а также прямую f с уравнением Ах+Ву+С=0 (коэффициенты А, В, С приведены в таблице 6). Построить на плоскости образ прямой f и найти его уравнение. При этом же аффинном преобразовании найти образ Z2 точки Z1(4, 4) двумя способами: графическим (применяя простое отношение трех точек некоторой прямой) и аналитическим (используя формулы пересчета координат, то есть предварительно найдя коэффициенты уравнений (19) по известным ∆М1L1P1 и ∆М2L2P2 ).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.