Определение многочлена. Схема Горнера и теорема Безу. Поле отношений. Отношение делимости в кольцах

 , ; е)   , .

Упражнение 2. Ответ: а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) .

Упражнение 3. Ответ: а) 

б) 

Упражнение 4. Ответ: а) ; ; б) ; .

Упражнение 5. Решение. .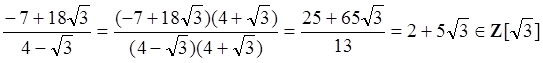

Упражнение 6. Решение. Для доказательства надо найти число , такое,  что . Раскрывая скобки, получаем, что . Это равенство может иметь место лишь при условии, что x, y, z удовлетворяют системе уравнений: 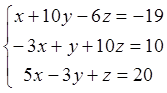. Решая эту систему, получаем, что .

Упражнение 7. Указание. Воспользоваться тем, что число  обратимо в .

Упражнение 8. Ответ: нет, да.

Упражнение 9. Ответ: да, частным  является число .

Упражнение 10. Указание. Воспользуйтесь тем, что элемент  обратим в кольце .

Упражнение 12. Ответ: 1) (1); 2) (12); 3) (12); 4) (3); 5) (4); 6) (3); 7) (6); 8) (18); 9) (1); 10) (2); 11) (2); 12) (12); 13) (24); 14) (2); 15) (3).

Упражнение 13. Ответ: 1) ;

2) ;

3) ;

4) ;

5)  ;

6)  ;

7) ;

8) ;

9) ;

10) ;

11) ;

12) .

13) ;

14) ;

15) .

Упражнение 14. Ответ: 1) -4; 2) 2; 3) ; 4) -3, ; 5) 0, 9; 6) 0; 7) 1, -2; 8) -2; 9) 0, -2; 10) -2; 11) 2, ; 12) -1; 13) 1, 0, 2, -1; 14) 2, 3, -1, 1.

Упражнение 17. Ответ: а) ; б) ; в) .

Упражнение 18. Ответ: а) ; б) .

Упражнение 19. Ответ: , , , .

Упражнение 20. Ответ: 1)  ; 2); 3); 4); 5) ;  6); 7); 8); 9); 10) .

Задача 2. Ответ: нет.

Задача 3. Решение. 1) .

2) Если ненулевой элемент , то . А равенство  возможно только тогда, когда  и , т.е. когда . Поэтому .

3) Найдем все делители числа 4. Если , то , откуда . Значит, . Все возможные значения a и b, при которых это имеет место, выписаны в следующую таблицу:

Следовательно, делители числа 4 находятся среди чисел ±1, , , ±2, ±4. Проверкой устанавливаем, что делителями числа 4 являются ±1, , ±2, ±4.

4) Среди чисел, приведенных в п.3, ±1, , ±2 являются делителями числа .

5) Ни один среди общих делителей чисел 4 и  не делится на все другие.

6) Если искать делители числа  так, как делается выше, то получим, что это числа, модули которых равны 1 или 2. Такие числа нетрудно перебрать и удостовериться, что делители числа  в  - это только оно само, противоположное ему и ±1.

7) .

8) Пусть  - необратимый элемент. Тогда он приводим, если  (так как это равенство в действительности невозможно, если u необратим). Воспользуемся индукцией по . Предположим, что приводим каждый необратимый элемент v, для которого . Если u приводим, то нечего доказывать. В противном случае , где  и . По индуктивному предположению, u₁ и u₂, а следовательно, и u являются конечными произведениями неприводимых множителей.

Задача 5.  Ответ. .

Задача 6. Решение. . В силу ограничений, наложенных на , это равенство при   дает .

Задача 7. Решение. Легко видеть, что . Если допустить, что c – кратный корень многочлена f(x), то  влечет  и . Но нуль не является корнем f(x).

Задача 8. Ответ: .

Задача 9. Ответ: , .

Задача 10. Решение. Производная  не имеет кратных корней, кроме 0.

Литература

1.   Алгебра и теория чисел: Учеб. пособие для студентов-заочников II курса физ.-мат. фак. пед. ин-тов (Н.А.Казачек, Г.Н.Перлатов, Н.Я.Виленкин, А.И.Бородин; Под ред. Н.Я.Виленкина. - 2-е изд. - М.: Просвещение, 1984. - 192с.

2.   Винберг Э.Б. Алгебра многочленов: Учебное пособие для студентов-заочников 3-4 курсов физико-математических факультетов педагогических институтов. - М.: Просвещение, 1980. - 175с.

3.   Ленг С. Алгебра. - М.: Мир, 1968. - 564с.

4.   Куликов Л.Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтв. - М.: Высш. школа, 1979. - 559с.

5.   Курош А.Г. Курс высшей алгебры. - М.: Наука, 1971. - 432с.

6.   Фаддеев Д.К. Лекции по алгебре: Учебное пособие для вузов. - М.: Наука. Главная редакция физико-математической литературы, 1984. - 416 с.

7.   Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Наука, 1968. – 304с.

8.   Шнеперман Л.Б. Сборник задач по алгебре и теории чисел./Учеб. Пособие для физ.-мат. факультетов пед. ин-тов. – Мн.: Высш. школа, 1982. 223с.

Содержание

1. Определение многочлена  ……………………………………….    стр. 3

2. Схема Горнера и теорема Безу  …………………………………    стр. 7

3. Поле отношений  ………………………………………………….   стр. 9

4. Отношение делимости в кольцах

4.1. Понятие делимости и его основные свойства  ………………   стр. 14

4.2. Идеалы  …………………………………………………………  стр. 18

4.3. Делимость в кольцах главных идеалов ………………………   стр. 22

4.4. Делимость многочленов  ………………………………………  стр. 25

5. Вычисление наибольшего общего делителя и

коэффициентов его линейного выражения. Результант.

5.1. Вычисление наибольшего общего делителя  ………………… стр. 27

5.2. Наименьшее общее кратное  …………………………………..  стр. 30

5.3. Результант  ……………………………………………………...  стр. 31

6. Производная многочлена. Формула Тэйлора.

6.1. Производная многочлена   ……………………………………..  стр. 35

6.2. Формула Тэйлора   …………………………………………….    стр. 36

6.3. Отделение кратных множителей   …………………………….   стр. 38

7. Построение кольца многочленов от нескольких

переменных. Решение систем алгебраических уравнений.

7.1. Построение кольца многочленов от нескольких переменных   стр. 41

7.2. Решение систем алгебраических уравнений …………………  стр. 46

Ответы, указания, решения.  ………………………………………    стр. 48

Литература.  …………………………………………………………..   стр. 51