Математика \ Высшая математика

Движения плоскости. Простейшие виды движений плоскости. Параллельный перенос (вектор). Скользящее отражение, страница 4

2) Единственность. Конечно, существует много других способов совместить  два конгруэнтных треугольника. Однако, речь идет не об отображении одной фигуры на другую, а о преобразовании всей плоскости как бесконечного множества точек. Единственность понимаем в том смысле, что, если А1В1С1 отобразился в А2В2С2, то тем самым однозначно задано движение всей плоскости, т.е. предопределена судьба «всех точек, окружавших треугольник». Действительно, любая М1 может быть соотнесена с  А1В1С1 конкретными расстояниями до его вершин, так что в образах отыщется единственно возможное положение М2 с теми же расстояниями  до образов вершин. Итак, для любой точки М1 можно («привязываясь к треугольникам») построить засечками циркуля единственный образ М2 . Ч.т.д.

          Замечание. Если бы в теореме брали треугольники А1В1С1 и А2В2С2

с одинаковыми ориентациями, то первый этап преобразований (симметрия) не понадобился бы.                       

          Определение.  Движения  которые   сохраняют  ориентацию  фигур , называют движениями первого рода  и обозначают  D1 . Если же движение меняет ориентацию фигур, то его относят ко  второму роду (обозначение - D2).

Например, движениями первого рода являются поворот, параллельный перенос, тождественное преобразование плоскости. А скользящее отражение и осевая симметрия – это движения второго рода.   Другие примеры:           ,           ,               .

          Композиция движений, содержащая нечетное число осевых симметрий, является движением второго рода.

§ 1. 3.  Аналитическое представление движений

Выведем формулы пересчета координат точек при произвольном движении плоскости. Как мы знаем из доказанной теоремы, конкретное движение предъявляется  парой  конгруэнтных треугольников (образ и прообраз).   

      Рис.12              

Пусть это будут те же А1В1С1 и А2В2С2 , что и на рис.11. Теперь введем декартову систему координат, связанную с А1В1С1. Назначим в А1 начало координат, ось Ох направим вдоль А1С1 (рис. 12). Именно такой выбор осей позволит применять ранее найденные для простейших движений системы уравнений (1),(2),(4).

Пусть произвольная точка М1 имела координаты (x1, y1) и при движении отобразилась в М2(x2, y2). Будем искать зависимость между «новыми» и «старыми» координатами. Для общности полагаем, что движение – второго рода.

Используем рассмотренную в теореме композицию отображений (симметрия – поворот – параллельный перенос), пересчитывая на каждом этапе координаты промежуточных образов, которые обозначим  М3(x3, y3)  и  М4(x4, y4). Итак, будем следить уже не за треугольниками, а за последовательными отображениями выбранной произвольной точки  М1.

1) Симметрия     происходит относительно оси  Ох, поэтому можно применить формулы типа (1) :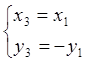

2) Поворот    происходит на угол α вокруг начала А1 координат, поэтому справедливы формулы типа (4):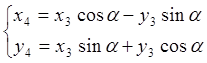 

3) Параллельный перенос   задан направленным отрезком , координаты которого в выбранной нами системе будут конкретными числами (их можно «измерить» на чертеже), допустим, (a, b). Тогда в силу системы (2)  получим  соотношения      .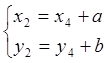       

Комбинируя три системы уравнений, найдем сквозную зависимость новых координат (x2, y2) от старых (x1, y1). При этом постараемся учесть не только рассмотренный случай  D2 ,  но  и случай  D1 .  Для этого систему (1) искусственно представим в виде 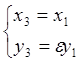                                     ,                             (5)

где число  ε  будем наделять подходящим значением  ε =-1 (для движений второго рода - D2) либо  ε = 1  (для  движений первого рода - D1). В результате система (5) задает либо симметрию, либо тождественное преобразование, а итоговая зависимость имеет вид

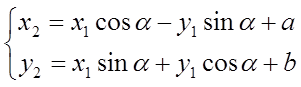                        (6)

Система  (6) задает аналитическое представление произвольного движения.

Эти формулы позволяют, перебирая всевозможные пары чисел (x1, y1), находить координаты (x2, y2) образов точек.

Частными случаями системы (6) (при обнулении , а, b) могут быть формулы (2), (4), (1) – для простейших видов движений.

                § 1. 4.  Классификация движений плоскости

Скачать файл