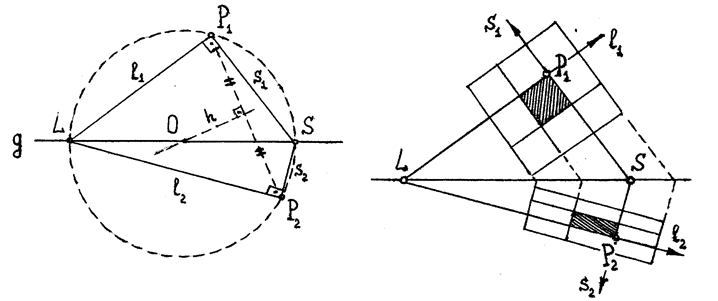
а) Рис.54 б)
Замечание. Прямые l1 и s1 (рис.54, б) задают главные направления родства. Ориентированная в этом направлении квадратная сетка будет отображаться в сетку прямоугольную. В каждой точке плоскости главные направления родства единственны.
Вывод. При родстве искажаются размеры фигур и углы, но сохраняется деление отрезков в заданном отношении, а также свойство прямых (или отрезков) быть параллельными.
Найдем формулы пересчета координат точек при родстве для случая, когда ось х совпадает с осью g родства (Рис.55).
|
Рис.55 |
Две точки, задающие преобра- зование (В1 и В2), заранее указаны (то есть их координаты можно «измерить по чертежу»). В записи В1(q1, m1) и В2(q2, m2) полагаем известными числа q1, m1, q2, m2. Для произвольной точки С1(x1, y1) найдем координаты x2, y2 образа С2 , то есть отыщем связь между «новыми» координатами x2, y2 и «старыми» x1, y1 . Для этого переведем на язык координат свойства взаимного расположения точек (рис. 55): |
а) Векторы 
и 
параллельны,
поэтому их координаты будут пропорциональными :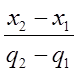 
= 
(
* ) .
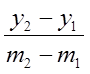б) Из подобия прямоугольных
треугольников (Рис.55) следует пропорциональность их сторон, значит 
= 
,
= 
.
в) При родстве сохраняется
простое отношение трех точек одной прямой, поэтому =
. Следовательно, и = (
** ) .
Из условия ( ** ) выражаем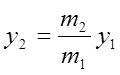 
и подставляем в ( * ) ,
получая после преобразований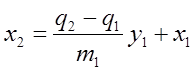 
. Вводя для
удобства новые обозначения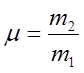 
, 
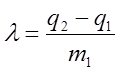, записываем
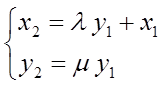(17)
( аналитическое представление родства с осью ОХ ) .
Можно заметить, что при λ = 0 и μ = -1 уравнения (17) совпадут с уравнениями (1) (см. §1.1), то есть осевая симметрия является частным случаем родства.
§ 3.2. Общие свойства аффинных преобразований.
Замечание 1. При аффинном преобразовании образом произвольного отрезка будет тоже отрезок.
Доказательство вытекает из определения: аффинное преобразование сохраняет коллинеарность точек, значит прямая отобразится в прямую. Кроме того, сохраняется простое отношение трех точек. Поэтому к двум концам произвольного отрезка третья точка (если она внутренняя) даст отрицательное простое отношение, что повторится и в образах. Значит, внутренние точки отрезка перейдут во внутренность нового отрезка. Ч.т.д.
Замечание 2. При аффинном преобразовании образом произвольного параллелограмма будет тоже параллелограмм.
Доказательство. Согласно замечанию 1, стороны параллелограмма перейдут в стороны нового четырехугольника, диагонали – в диагонали. В параллелограмме точка пересечения диагоналей делит их пополам. Это отношение должно сохраниться, то есть диагонали нового четырехугольника будут в пересечении делиться пополам, что является достаточным признаком параллелограмма.Ч.т.д.
Замечание 3. При аффинном преобразовании образами параллельных прямых будут тоже параллельные прямые.
Доказательство. Если вписать в полосу между параллельными прямыми параллелограмм, то его образом, согласно замечанию 2, будет тоже параллелограмм. В результате образы прямых будут содержать противоположные стороны нового параллелограмма, что означает их параллельность. Ч.т.д.
Следствие. При аффинном преобразовании образом квадратной координатной сетки будет «сетка из параллелограммов».
Действительно, при сохранении простого отношения трех точек середины отрезков перейдут в середины, равномерный ряд точек – в равномерный, общие стороны квадратов – в общие стороны параллелограммов (рис.56).
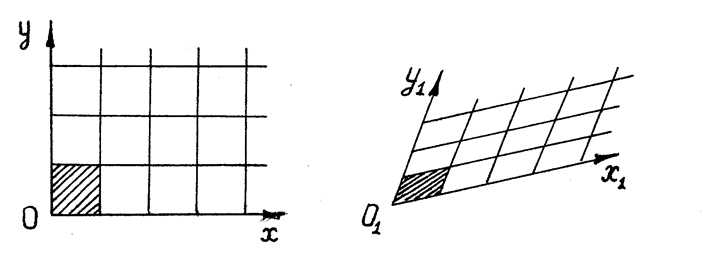
Рис.56
Косоугольную координатную систему поэтому называют «аффинной».
Замечание 4. При аффинном преобразовании сохраняется отношение площадей фигур в их образах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
