Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
Кафедра автоматики и вычислительной техники
по лабораторной работе №1
Дисциплина: идентификация и диагностика систем управления
Тема: моделирование случайных факторов.
Вариант: 22
Выполнил студент гр. 5081/11
Проверил:
Санкт-Петербург
2010
Задание
1. Провести моделирование генерации нормально-распределенных чисел для следующих значений математического ожидания и дисперсии:
|
математическое ожидание |
0 |
0 |
1 |
|
дисперсия |
1 |
4 |
4 |
Выяснить зависимость оценок (точечных и интервальных)
математического ожидания и дисперсии от объема выборки (![]() ) при доверительном
уровне
) при доверительном
уровне ![]() .
.
2. Определить объемы выборки, необходимые для получения
доверительного интервала математического ожидания, равного 0,1 при
доверительном уровне ![]() . Провести моделирование
для полученного значения объема выборки.
. Провести моделирование
для полученного значения объема выборки.
3. Провести моделирование генерации вектора нормально-распределенных чисел при размерности 2 и нулевом математическом ожидании для следующих значений корреляционных матриц:
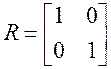 ,
, 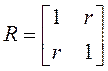 ,
, 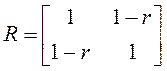 ,
, 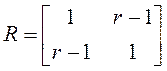 .
.
Построить оценки заданной корреляционной матрицы и выяснить зависимость оценок от объема выборки.
Построить доверительные интервалы для оценки коэффициента
корреляции в зависимости от объема выборки ![]() , при доверительном
уровне
, при доверительном
уровне ![]() .
.
4. Провести моделирование генерации случайного процесса,
представленного уравнением авторегрессии 1 порядка. Определить оценку
коэффициента авторегрессии ![]() для
случаев из таблицы вариантов.
для
случаев из таблицы вариантов.
5. Для каждого коэффициента авторегрессии ![]() определить коэффициент
авторегрессии
определить коэффициент
авторегрессии ![]() для
получения процесса авторегрессии 2 порядка, исходя из условия стационарности
случайного процесса.
для
получения процесса авторегрессии 2 порядка, исходя из условия стационарности
случайного процесса.
6. Провести моделирование генерации случайного процесса,
представленного уравнением авторегрессии 2 порядка. Определить оценку
коэффициентов авторегрессии ![]() и
и ![]() .
.
7. Сформулировать выводы о проделанной работе, оформить отчет.
|
Вариант |
|
|
|
|
22 |
0,2 |
0,15 |
0,6 |
1. Моделирование генерации нормально-распределенных чисел.
Точечные оценки случайной выборки - медиана, отклонение
(девиация), оценка математического ожидания ![]() и дисперсии
и дисперсии ![]() (среднеквадратического
отклонения
(среднеквадратического
отклонения ![]() ):
):
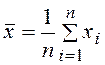
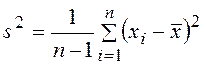
Интервальные оценки:
Оценка доверительного интервала для математического ожидания:
![]() ,
,
![]() –
– ![]() -процентный квантиль
распределения Стьюдента с
-процентный квантиль
распределения Стьюдента с ![]() степенями
свободы.
степенями
свободы.
![]() –
объем выборки
–
объем выборки
Q – доверительная вероятность.
Оценка доверительного интервала для дисперсии:
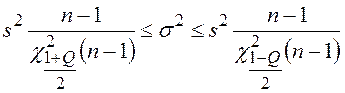
![]() –
– ![]() -процентный квантиль
распределения Хи-квадрат с
-процентный квантиль
распределения Хи-квадрат с ![]() степенями
свободы.
степенями
свободы.
1.1. Моделирование генерации нормально-распределенных чисел
1_1.m
clear all;
M = 0; %0 0 1
D = 1; %1 4 4
N = 10; %10 20 50 100 1000
t = 0:0.01:N;
x = normrnd(M, D, 1, N);
MTmp = mean(x);
DTmp = std(x);
figure
plot(x,'k')
hold on
grid on
figure
hist(x,1000)
grid on
.
1.2.
Выяснение зависимости оценок
(точечных и интервальных) математического ожидания и дисперсии от объема выборки
(![]() ) при доверительном
уровне
) при доверительном
уровне ![]() .
.
1_2.m
clear all;
N = [10,20,50,100,1000];
M = 0; % 0 0 1
D = 1; % 1 4 4
q = [0.9, 0.95];
aver = zeros(1,5);
dev = zeros(1,5);
for i=1:5
x = normrnd(M,D,1,N(i));
aver(i) = mean(x);
dev(i) = std(x);
end
% матрицы для доверительных интервалов
M9 = zeros(2,5);
M95 = zeros(2,5);
hold on
for i=1:5
M9(1,i) = aver(i)-tinv((1+q(1))/2, N(i)-1)*dev(i)/sqrt(N(i));
M9(2,i) = aver(i)+tinv((1+q(1))/2, N(i)-1)*dev(i)/sqrt(N(i));
M95(1,i) = aver(i)-tinv((1+q(2))/2, N(i)-1)*dev(i)/sqrt(N(i));
M95(2,i) = aver(i)+tinv((1+q(2))/2, N(i)-1)*dev(i)/sqrt(N(i));
end
D9 = zeros(2,5);
D95 = zeros(2,5);
hold on
for i=1:5
D9(1,i) = sqrt((dev(i)^2)*(N(i)-1)/chi2inv((1+q(1))/2,N(i)-1));
D9(2,i) = sqrt((dev(i)^2)*(N(i)-1)/chi2inv((1-q(1))/2,N(i)-1));
D95(1,i) = sqrt((dev(i)^2)*(N(i)-1)/chi2inv((1+q(2))/2,N(i)-1));
D95(2,i) = sqrt((dev(i)^2)*(N(i)-1)/chi2inv((1-q(2))/2,N(i)-1));
end
disp('N: 10 20 50 100 1000');
disp(' ');
disp('Интервальная оценка мат. ожидания:');
disp('q = 0.9');
disp(M9);
disp('q = 0.95');
disp(M95);
disp('Интервальная оценка дисперсии:');
disp('q = 0.9');
disp(D9);
disp('q = 0.95');
disp(D95);
disp('Точечная оценка мат. ожидания:');
disp(aver);
disp('Точечная оценка дисперсии:');
disp(dev);
plot(N, M9(1,:),'ko',N, M95(1,:),'r*', N, aver, 'b+', N, M9(2,:),'ko', N, M95(2,:),'r*',[10,1000],[M,M]);
xlabel('n');
ylabel('M');
legend('Интервальная оценка мат. ожидания, q = 0.9','Интервальная оценка мат. ожидания, q = 0.95', 'Точечная оценка мат. ожидания');
figure
plot(N, D9(1,:),'ko',N, D95(1,:),'r*', N, dev,'b+', N, D9(2,:),'ko',N, D95(2,:),'r*',N,dev,'b+',[10,1000],[D,D]);
xlabel('n');
ylabel('D');
legend('Интервальная оценка дисперсии, q = 0.9','Интервальная оценка дисперсии, q = 0.95', 'Точечная оценка дисперсии');
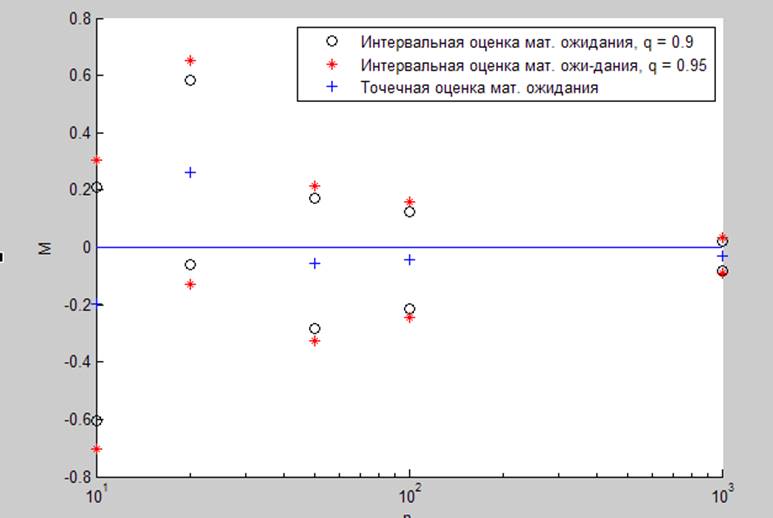
Рис. 1.2.1. Оценка математического ожидания для различных выборок при (0,1).
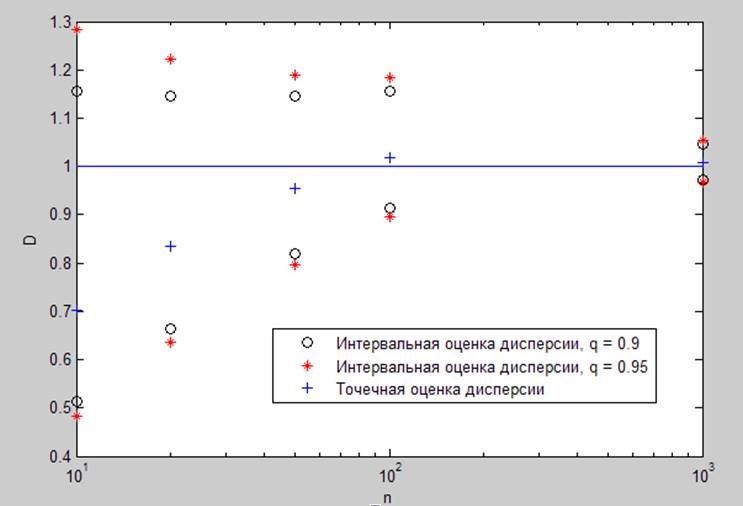
Рис. 1.2.2. Оценка дисперсии для различных выборок при (0,1).
N: 10 20 50 100 1000
Интервальная оценка мат. ожидания:
q = 0.9
-0.6063 -0.0612 -0.2817 -0.2130 -0.0817
0.2088 0.5852 0.1709 0.1255 0.0233
q = 0.95
-0.7017 -0.1292 -0.3267 -0.2460 -0.0917
0.3042 0.6533 0.2158 0.1585 0.0334
Интервальная оценка дисперсии:
q = 0.9
0.5128 0.6637 0.8202 0.9137 0.9727
1.1567 1.1456 1.1469 1.1555 1.0470
q = 0.95
0.4836 0.6357 0.7972 0.8950 0.9660
1.2836 1.2210 1.1893 1.1842 1.0546
Точечная оценка мат. ожидания:
-0.1987 0.2620 -0.0554 -0.0438 -0.0292
Точечная оценка дисперсии:
0.7031 0.8360 0.9544 1.0194 1.0084
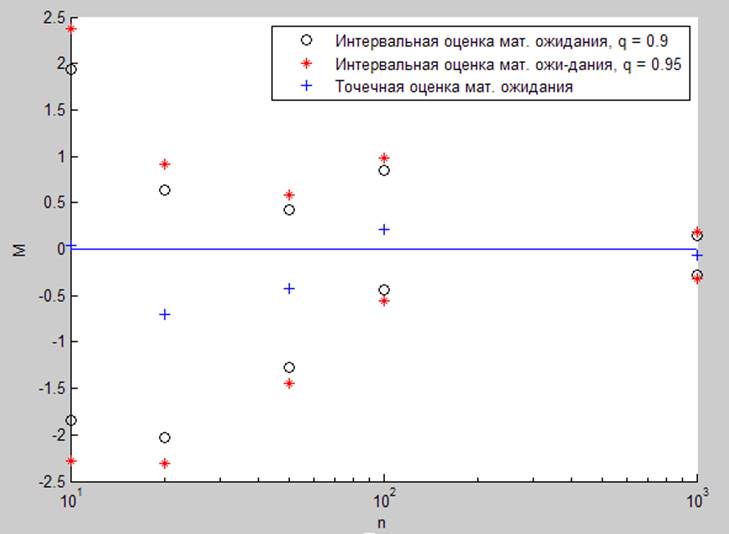
Рис. 1.2.3. Оценка математического ожидания для различных выборок при (0,4).
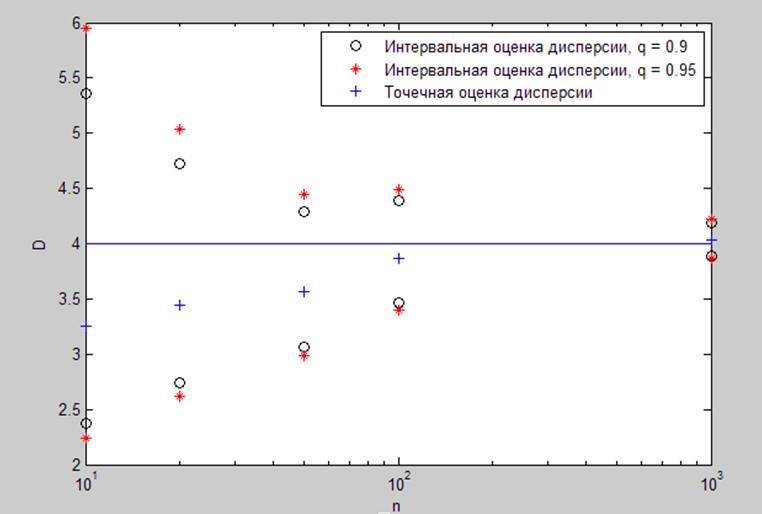
Рис. 1.2.4. Оценка дисперсии для различных выборок при (0,4).
N: 10 20 50 100 1000
Интервальная оценка мат. ожидания:
q = 0.9
-1.8418 -2.0310 -1.2738 -0.4313 -0.2763
1.9332 0.6347 0.4194 0.8533 0.1437
q = 0.95
-2.2836 -2.3115 -1.4420 -0.5566 -0.3166
2.3750 0.9152 0.5876 0.9786 0.1840
Интервальная оценка дисперсии:
q = 0.9
2.3748 2.7368 3.0687 3.4673 3.8906
5.3570 4.7241 4.2909 4.3850 4.1878
q = 0.95
2.2397 2.6216 2.9827 3.3964 3.8640
5.9444 5.0349 4.4495 4.4938 4.2183
Точечная оценка мат. ожидания:
0.0457 -0.6981 -0.4272 0.2110 -0.0663
Точечная оценка дисперсии:
3.2561 3.4472 3.5706 3.8684 4.0333
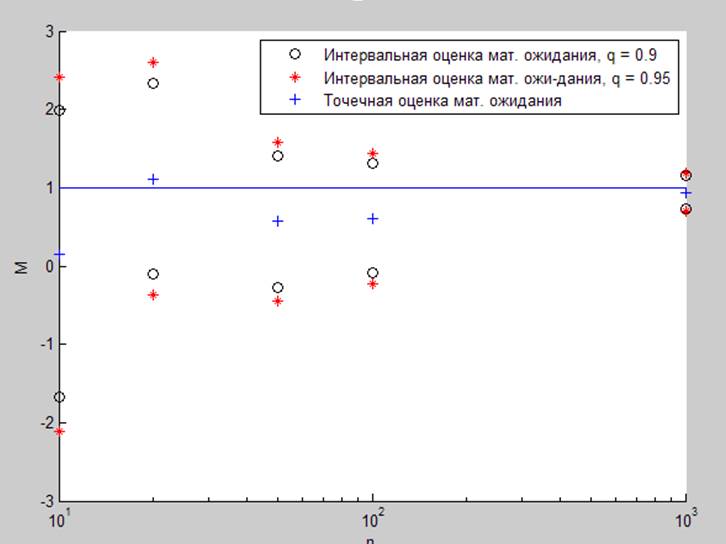
Рис. 1.2.5. Оценка математического ожидания для различных выборок при (1,4).
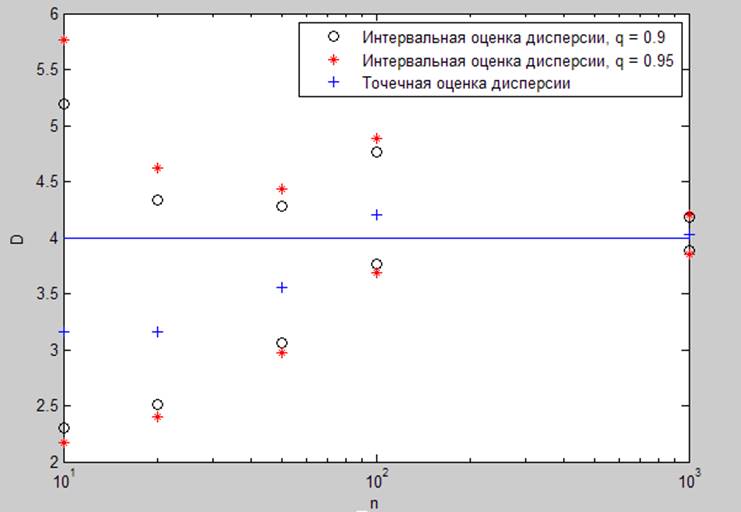
Рис. 1.2.6. Оценка дисперсии для различных выборок при (1,4).
N: 10 20 50 100 1000
Интервальная оценка мат. ожидания:
q = 0.9
-1.6790 -0.1095 -0.2763 -0.0866 0.7317
1.9820 2.3361 1.4110 1.3084 1.1507
q = 0.95
-2.1074 -0.3668 -0.4439 -0.2226 0.6915
2.4104 2.5934 1.5786 1.4444 1.1909
Интервальная оценка дисперсии:
q = 0.9
2.3031 2.5108 3.0582 3.7652 3.8816
5.1951 4.3340 4.2762 4.7617 4.1781
q = 0.95
2.1720 2.4051 2.9724 3.6882 3.8550
5.7648 4.6191 4.4342 4.8798 4.2085
Точечная оценка мат. ожидания:
0.1515 1.1133 0.5673 0.6109 0.9412
Точечная оценка дисперсии:
3.1578 3.1625 3.5584 4.2007 4.0240
2. Определение объема выборки, необходимого для получения
доверительного интервала математического ожидания, равного 0,1 при
доверительном уровне
![]() .
.
Объем выборки для оценки математического ожидания:
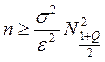
clc
q=[0.9, 0.95];
X_9=zeros(2,1);
X_95=zeros(2,1);
M=0;
D=1;
h=0.1;
n1 = 1057;
n2 = 1480;
n_90_min=(D/(h/2)^2)*(1.282)^2
n_90 = n1
x = normrnd(M,D,1,n1);
Xsr=mean(x);
S2=std(x)^2;
X_9_l = Xsr-tinv((1+q(1))/2, n1-1)*S2/sqrt(n1);
X_9_h = Xsr+tinv((1+q(1))/2, n1-1)*S2/sqrt(n1);
interval_90=X_9_h-X_9_l
n_95_min=(D/(h/2)^2)*(1.645)^2
n_95 = n2
x=normrnd(M,D,1,n2);
Xsr=mean(x);
S2=std(x)^2;
X_95_l = Xsr-tinv((1+q(2))/2, n2)*S2/sqrt(n2);
X_95_h = Xsr+tinv((1+q(2))/2, n2)*S2/sqrt(n2);
interval_95=X_95_h-X_95_l
n_90_min = 657.4096
n_90 =1057
interval_90 = 0.1005
n_95_min = 1.0824e+003
n_95 =1480
interval_95 = 0.1045
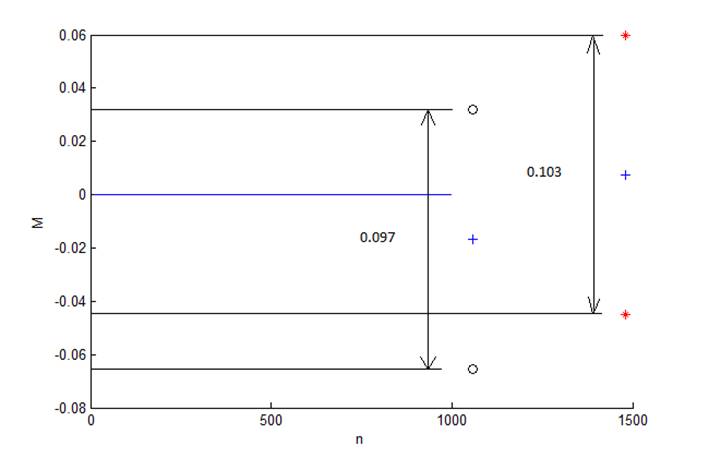
Рис. Моделирование для полученных значений выборки
3. Провести моделирование генерации вектора нормально-распределенных чисел при размерности 2 и нулевом математическом ожидании для следующих значений корреляционных матриц:
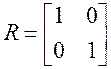 ,
, 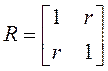 ,
,  ,
, 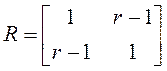 .
.
Построить оценки заданной корреляционной матрицы и выяснить зависимость оценок от объема выборки.
Построить доверительные
интервалы для оценки коэффициента корреляции в зависимости от объема выборки ![]() , при доверительном
уровне
, при доверительном
уровне ![]() .
.
r = 0,2
Многомерное нормальное распределение вектора:
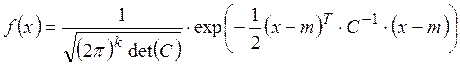
![]()
![]()
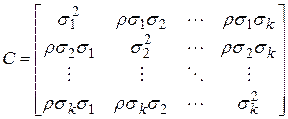
где mi – математическое ожидание хi,
С – ковариационная матрица
Двумерное нормальное распределение:
![]()
Распределение моделируется с помощью линейного преобразования Х=Аy+mx; А определяется условием С=А*АТ, где А – нижнетреугольная матрица.
В Matlab определение А производится на основе разложения Хорецкого с помощью функции R = chol(r), дающей значение матрицы А – верхнетреугольной матрицы.
Приближенный доверительный
интервал для коэффициента корреляции двумерного нормального распределения,
коэффициент корреляции ![]() неизвестен.
неизвестен.
![]() – оценка
– оценка ![]() .
.
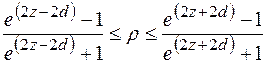 ,
,
![]() ,
,
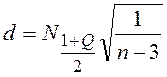 .
.
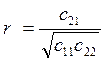
![]() –
– ![]() -процентный квантиль
нормального распределения.
-процентный квантиль
нормального распределения.
3.m
clear all
r = -0.82; % 0 0.18 0.82 -0.82
R = [1,r;r,1];
N = [10,20,50,100,1000];
a = [0.9,0.95];
R9 = zeros(2,5);
R95 = zeros(2,5);
r_coeff = zeros(1,5);
q1 = chol(R);
q = q1';
for i=1:5
z1 = zeros(N(i),2);
z2 = z1;
for j=1:N(i)
x1 = randn(2,1);
z1(j,:) = x1';
x2 = q*x1;
z2(j,:) = x2';
end
r2 = cov(z2);
KK = r2(1,2)/sqrt(r2(1,1)*r2(2,2));
r_coeff(i) = KK;
z = 1/2*log((1+KK)/(1-KK));
d = norminv((1+a(1))/2)*sqrt(1/(N(i)-3));
R9(1,i)=(exp(2*z-2*d)-1)/(exp(2*z-2*d)+1);
R9(2,i)=(exp(2*z+2*d)-1)/(exp(2*z+2*d)+1);
d = norminv((1+a(2))/2)*sqrt(1/(N(i)-3));
R95(1,i)=(exp(2*z-2*d)-1)/(exp(2*z-2*d)+1);
R95(2,i)=(exp(2*z+2*d)-1)/(exp(2*z+2*d)+1);
end
disp('N: 10 20 50 100 1000');
disp(' ');
disp('Интервальная оценка коэффициента корреляции:');
disp('q = 0.9');
disp(R9);
disp('q = 0.95');
disp(R95);
disp('Точечная оценка коэффициента корреляции:');
disp(r_coeff);
plot(N, R9(1,:),'ko',N, R95(1,:),'r*', N, r_coeff, 'b+', N, R9(2,:),'ko', N, R95(2,:),'r*',[10,1000],[r,r]);
legend('Интервальная оценка коэффициента корреляции, q = 0.9','Интервальная оценка коэффициента корреляции, q = 0.95', 'Точечная оценка коэффициента корреляции');
xlabel('n');
ylabel('R');
figure('color', 'white')
plot(z1(1:1000,1), z1(1:1000,2),'ro')
figure('color', 'white')
plot(z2(1:1000,1), z2(1:1000,2),'bo')
r = 0
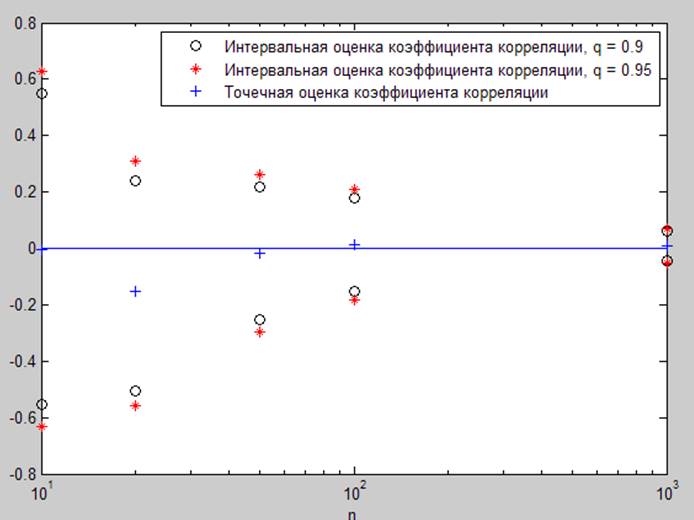
Рис.3.1. Интервальная оценка коэффициента корреляции для различного объема
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.