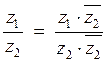Уводзіны. Элементы тэорыі мностваў і матэматычнай логікі. Рэчаісныя лікі, страница 5

 .

Правіла дзялення камплексных лікаў: каб падзяліць два камплексныя лікі , трэба лічнік і назоўнік дробу дамножыць на лік, камплексна-спалучаны назоўніку.

Прыклад 1. Вылічыць .

∆ ◄

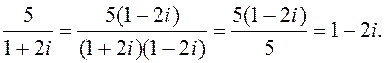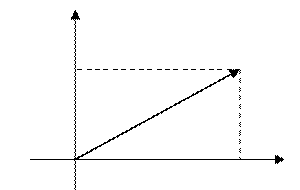
Увядзем на камплекснай плоскасці палярную сістэму каардынатаў так, каб яе полюс знаходзіўся ў пункце  прамавугольнай сістэмы каардынатаў, а палярная вось супадала з дадатным кірункам восі . З геаметрычных меркаванняў атрымаем формулы

, якія звязваюць палярныя і дэкартавыя каардынаты. Адсюль вынікае гэтак званая трыганаметрычная форма камплекснага ліку :

def: Лік  называецца модулем, а лік  – аргументам камплекснага ліку .

Аргумент камплекснага ліку  не вызначаны, а яго модуль роўны нулю. Зазначым, што аргумент  вызначаецца неадназначна, з дакладнасцю да складніка. Пры гэтым выкарыстоўваюцца абазначэнні  – алзін заргументаў,  – мноства ў сіх аргументаў ліку . Значэнне аргументу, якое праўдзіць няроўнасці , называецца галоўным.

З сістэмы 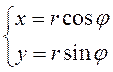  маем .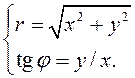

Зазначым, што з апошняй сістэмы аргумент камплекснага ліку знаходзіцца неадназначна, паколькі аргументы абодвух лікаў  і  з’яўляюцца развязкасмі гэтай сістэмы.

Заўвага 1. Пры вылічэнні аргумента камплекснага ліку з роўнасці  карыстаемся правілам:

Прыклад 2. Вызначыць трыганаметрычную форму камплексных лікаў: ;

∆ 1)     2)

3)  4)  ◄

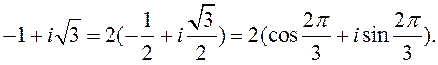Трыганаметрычная форма камплекснага ліку ёсць вельмі зручная для множання і дзялення камплексных лікаў. Няхай

.

Вылічым іх здабытак

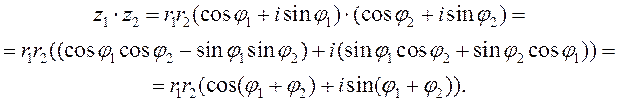
З гэтай роўнасці маем , г.зн. пры множанні камплексных лікаў іх модулі перамнажаюцца, а аргументы складваюцца. Аналагічна атрымліваецца: пры дзяленні камплексных лікаў іх модулі дзеляцца, а аргументы адымаюцца

.

Калі перамножыць  роўных камплексных лікаў, то атрымаецца

.

Пры  мае месца гэтак званая формула Муаўра

.

З геаметрычнага выяўлення камплексных лікаў вынікае правіла роўнасці камплексных лікаў ў трыганаметрычнай форме :

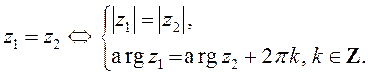
def: Камплексны лік  называецца коранем  й  ступені з камплекснага ліку  , , калі .

Атрымаем формулы для вылічэння кораня й ступені з камплекснага ліку . Няхай ,  З роўнасці  і формулы Муаўра вынікае  На падставе правіла роўнасці камплексных лікаў ў трыганаметрычнай форме атрымліваем

.

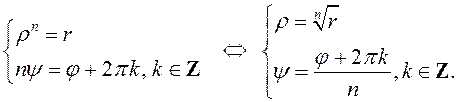Такім чынам, мы маем формулу           (2)

Пакажам, што сярод камплексных лікаў  маецца роўна  розных. Сапраўды, сярод камплексных лікаў , якія вылічаюцца паводле формулы (2) пры  усе розныя таму, што іх аргументы

розняцца адзін ад другога менш чым на  (– найбольшая з розніцаў). Тады адпаведна правілу роўнасці камплексных лікаў ў трыганаметрычнай форме ўсе ,  розныя. Затым атрымліваем , бо  і . Аналагічна . Такім чынам, маецца роўна  розных значэнняў кораня –й ступені з камплекснага ліку:

.

Прыклад 3. Вылічыць

∆  

 

  ◄

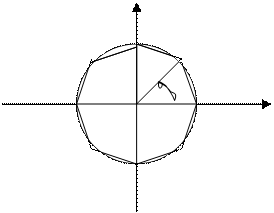
Заўвага 2. На камплекснай плоскасці пункты  размяшчаюцца ў вяршынях правільнага –вугольніка, умежанага ў акружыну радыюсу  з цэнтрам у пункце  таму, што ,

.

§1.4. Алгебра мнагаскладаў.

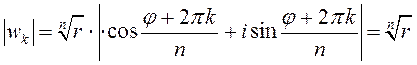def: Мнагаскладам або паліномам –й ступені называецца выраз

дзе  – камплексная зменная велічыня,  – камплексныя канстан-ты, прычым .

def: Мнагасклады  і  называюцца роўнымі , калі роўныя іх ступені  і роўныя адпаведныя каэфіцыенты

Мае месца наступная

Тэарэма 1 (пра выяўленне мнагаскладу). Калі ступень мнагаскладу  не меншая за ступень мнагаскладу , г.зн. , то існуюць такія два мнагасклады  і , , што

.                                              (1)

Для доказу тэарэмы разглядаюцца мнагасклады з нявызначанымі каэфіцыентамі ,  – не-вядомыя камплексныя лікі. Пасля падстаўлення гэтых мнагаскладаў ў (1), прывядзення падобных складнікаў і прыраўноўвання каэфіцыентаў пры аднолькавых ступенях  у абедзвюх частках атрыманай роўнасці, для знаходжання каэфіцыентай  і  будзем мець сістэму лінейных раўнанняў, з якой  і  вызначаюцца адзіным спосабам.

Звычайна дзель ад дзялення двух мнагаскладаў і адпаведную астачу знаходзяць метадам дзялення вугалком. Напрыклад,

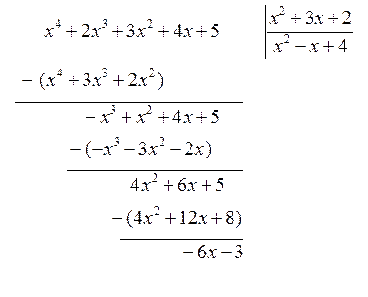
Пры гэтым мае месца роўнасць .

Дзяліць мнагасклад на двухсклад  зручна паводле схемы Горнера. Напрыклад, падзелім  на . Маем

.

Такім чынам, .