Уводзіны. Элементы тэорыі мностваў і матэматычнай логікі. Рэчаісныя лікі

Віктар Ахраменка

КУС ЛЕКЦЫЙ ПА МАТЭМАТЫЧНЫМ АНАЛІЗЕ

для студэнтаў радыёфізічнага факультэта

1 КУРС  1 СЕМЕСТР

БЕЛАРУСКІ ДЗЯРЖАЎНЫ УНІВЕРСІТЭТ

Літаратура:

1.  Валянцін Русак і інш. “Курс вышэйшай матэматыкі”,Мінск, 1994, !997.

2.  Α. -Крикоров, . “Курс математического анализа”.

3.  В.А.Ильин, Э.Г.Позняк. “Основы математического анализа”, ч.1,2.

4.  Л.Д.Кудрявцев. “Математический анализ”, т.1,2.

5.  Б.П.Демидович. “Сборник задач и упражнений по математическому анализу”.

6.   Н.Р.Абрашына-Жадаева, В.К.Ахраменка. “Вышэйшая матэматыка ў прыкладах і задачах. Матэматычны аналіз. Частка1.”

Раздзел 1. Уводзіны.

§1.1.  Элементы тэорыі мностваў і матэматычнай логікі.

Паняцце мноства ёсць адно з асноўных у матэматыцы. Яно належыць да так званых першасных паняццяў, якія не азначаюцца праз больш простыя. Пад мноствамразумеюць сукупнасць аб’ектаў, якія аб’ядноўваюцца ў адну групу па пэўным прыкметам.. Прыклады мностваў: мноства студэнтаў у аўдыторыі; мноства тых з іх, хто вывучаў у школе нямецкую мову.

Мноствы будзем абазначаць вялікімі літарамі: , а таксама . Аб’екты, з якіх складаецца мноства, называюцца яго элементамі. Запіс  азначае:  ёсць элемент мноства , або  належыць . Калі  не ёсць элемент мноства , то пішуць . Запіс  азначае, што мноства  ёсць канечнае і складаецца з  элементаў .

Калі кожны элемент мноства  ёсць элемент мноства , то пішуць  або  і мноства  называюць падмностваммноства . Пры гэтым кажуць, што  змяшчаецца ў , або  змяшчае . Калі існуе элемент  такі, што , то мноства  не з’яўляецца падмноствам мноства , што абазначаюць:  або .    Мноствы, якія складаюцца з адных і тых самых элементаў, называюцца роўнымі. Калі  і  роўныя мноствы, то пішуць .

Для вылучэння з мноства  падмноства  тых элементаў  , якія маюць пэўную ўласцівасць , выкарыстоўваюць запіс  (:–такі што).

Напрыклад, .

Можа атрымацца, што ні адзін элемент мноства  не мае ўласцівасці . Тады мноства  называецца пустым мноствам і абазначаецца . Напрыклад, . Пустое мноства лічыцца падмноствам усякага мноства.

Перасячэннем мностваў  і  называецца мноства  тых элементаў якія належаць як мноству , так і мноству .

Аб’яднаннем  мностваў  і  называецца мноства ўсіх тых элементаў, якія належаць прынамсі (хаця б) аднаму з мностваў  і  і абазначаецца .

Аперацыі перасячэння і аб’яднання мностваў добра ілюструюцца дыяграмамі Эйлера-Вена:

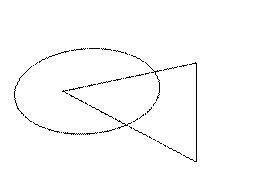
Аперацыі перасячэння і аб’яднання мностваў маюць уласцівасці:

1. 

2. 

3.  Калі , то

4.  ;

5.  .

Розніцаю мностваў  і  называецца мноства  усіх тых элементаў мноства , якія не належаць мноству . Маюць месца ўласцівасці:

.

Два элементы  і , , запісаныя ў выглядзе , будзем называць упарадкаванаю параю. Дзве пары  і  называюцца роўнымі, калі і толькі калі . Калі , то .

Мноства, элементамі якога з’яўляюцца ўсе ўпарадкаваныя пары , , называецца дэкартавым здабыткам мностваў  і  і абазначаецца . Калі, напрыклад,  то ,  . Відочна, што .

Пытанне: Калі  ?  (Калі і толькі калі .)

Дайце геаметрычнае выяўленне дэкартавага здабытка .

Няхай зададзены два мноствы  і . Няхай кожнаму элементу  пастаўлены ў адпаведнасць пэўны элемент . Саму адпаведнасць будзем абазначаць літараю , а тое, што элемент пры гэтай адпаведнасці пераходзіць у элемент , будзем запісваць сімвалічна так: , або . Такую адпаведнасць  будзем называць адлюстраваннем мноства  у мноства  або функцыяй з  мноства  у мноства .

Прыклад 1. Няхай – мноства натуральных лікаў, а  ёсць мноства, якое складаецца з двух лікаў 0 і 1. Пабудуем адлюстраванне мноства  у мноства , або функцыю з мноства  у мноства .

Дзеля гэтага выкарыстаем наступную формулу

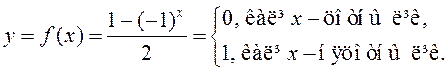                     (1)

Няхай функцыя   вызначана на мностве  і адлюстроўвае мноства  у мноства . Праз  будзем абазначаць мноства ўсіх тых элементаў з , якія з’яўляюцца значэннямі функцыі прынамсі пры адным . Мноства  будзем называць мноствам значэнняў функцыі  на мностве . Зразумела, што . Калі ж , г.зн. кожны элемент мноства  ёсць значэнне функцыі  пры некаторым , то кажуць, што функцыя  адлюстроўвае  на .

Калі  і пры любых ,  таксама , то адлюстраванне мноства  на мноства  называецца узаемна адназначным.

У гэтым выпадку на мностве  можна вызначыць функцыю  , ставячы ў адпаведнасць кожнаму элементу  такі элемент , што . Гэтая функцыя называецца адваротнаю функцыяй да функцаі  і абазначаецца . Функцыі  і  называюцца пры гэтым узаемна адваротнымі.

Прыклад 2. Адлюстраванне (1) мноства  на мноства  не ёсць узаемна адназначным, але тая ж функцыя (1) адлюстроўвае мноства  на мноства  узаемна адназначна. Прывядзіце прыклад функцыі , якая адлюстроўвае мноства  на мноства  (г.зн. адваротную да функцыі (1)). ()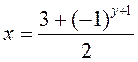

Калі існуе узаемна адназначнае адлюстраванне мноства  на мноства , то мноствы  і  называюцца эквівалентнымі, а іх эквівалентнасць запісваецца так.  Пры якой умове два канечныя мноствы эквівалентныя? (Калі яны змя шчаюць аднолькавую колькасць элементаў).

Прыклад 3.  Разгледзім мноствы  і – мноства цэлых лікаў. Зразумела, што . Установім узаемна адназначную адпаведнасць паміж элементамі мностваў  і . Кожнаму няцотнаму ліку  з  паставім у адпаведнасць лік  з мноства , а цотнаму ліку  з  паставім у адпаведнасць лік  з . Такім чынам, функцыя