►Дамножым гэтую роўнасць на ![]() , калі
, калі ![]() .
Паколькі
.
Паколькі ![]() , то
, то
![]() ,
адкуль
,
адкуль 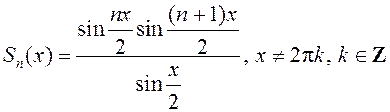 .
Калі ж
.
Калі ж ![]() , то
, то ![]() .◄
.◄
►Патрэбна даказаць роўнасць
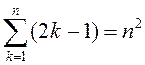 . (1.2)
. (1.2)
Скарыстаем метад матэматычнай індукцыі.
1) Формула (1.2) праўдзіцца для n= 1, бо 1 = 1.
2) Няхай ![]() – адвольны натуральны
лік і для
– адвольны натуральны
лік і для ![]() роўнасць (1.2) ёсць
праўдзівая, г. зн.
роўнасць (1.2) ёсць
праўдзівая, г. зн. 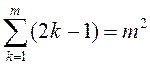 . Дакажам, што з
гэтага вынікае праўдзі-васць (1.2) для
. Дакажам, што з
гэтага вынікае праўдзі-васць (1.2) для ![]() .
Сапраўды,
.
Сапраўды,
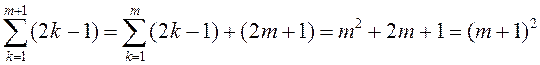 .
.
Гэта азначае, што роўнасць (1.2) даказана для кожнага натуральнага n. ◄
![]() . (1.3)
. (1.3)
►Сцверджанне, якое можна было б даказваць
метадам матэматычнай індукцыі яўна не сфармулявана. З гэтай прычыны высветлім
закана-мернасць узаемадачыненняў велічыняў ![]() i
i ![]() . Нададзім паслядоўна
ліку n значэнні
. Нададзім паслядоўна
ліку n значэнні ![]() i адпаведна атрымаем
i адпаведна атрымаем ![]()
![]()
![]()
![]()
![]() .
Такім чынам, можна выказаць гіпотэзу: няроўнасць (1.3) праўдзіцца для кожнага
натуральнага
.
Такім чынам, можна выказаць гіпотэзу: няроўнасць (1.3) праўдзіцца для кожнага
натуральнага ![]() . Дакажам гэтае сцверджанне.
. Дакажам гэтае сцверджанне.
1) Праўдзівасць базы індукцыі для ![]() ужо даказана.
ужо даказана.
2) Дапусцім, што
няроўнасць (1.3) праўдзіцца для адвольнага ![]()
![]() , г. зн.
, г. зн.
![]() . (1.4)
. (1.4)
Скарыстоўваючы няроўнасць (1.4), дакажам няроўнасць
![]() . (1.5)
. (1.5)
Зыходзячы з няроўнасці (1.4), маем ![]() . Калі мы пакажам што
. Калі мы пакажам што ![]() , то гэта і будзе азначаць
праўдзівасць няроўнасці (1.5). Сапраўды, апошняя няроўнасць раўназначная
няроўнасці
, то гэта і будзе азначаць
праўдзівасць няроўнасці (1.5). Сапраўды, апошняя няроўнасць раўназначная
няроўнасці ![]() , або
, або ![]() , якая пры
, якая пры ![]() ёсць праўдзівая, а тым самым
праўдзіцца няроўнасць (1.5). Згодна з метадам матэматычнай індукцыі мы
даказалі, што няроўнасць (1.3) праўдзіцца для кожнага
ёсць праўдзівая, а тым самым
праўдзіцца няроўнасць (1.5). Згодна з метадам матэматычнай індукцыі мы
даказалі, што няроўнасць (1.3) праўдзіцца для кожнага ![]() і таксама
пераканаліся ў яе праўдзівасці для n=1. ◄
і таксама
пераканаліся ў яе праўдзівасці для n=1. ◄
1.1.
Няхай А – мноства дзельнікаў ліку 15; В
– мноства простых лікаў, меншых за 10; С – мноства цотных лікаў, меншых
за 9. Знайдзіце мноствы: 1) ![]() ;
2)
;
2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() .
.
1.2.
Няхай А = [–2, 3], В = (–∞, 0), С
= [0, 4). Знайдзіце мноствы:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() і выявіце іх на лікавай прамой.
і выявіце іх на лікавай прамой.
1.3.
Няхай мноствы А = (–![]() , 2] і В = [–3, 5) ёсць
падмноствы універсаль-нага мноства
, 2] і В = [–3, 5) ёсць
падмноствы універсаль-нага мноства ![]() . Знайдзіце мноствы:
1)
. Знайдзіце мноствы:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() і вы-явіце іх на
лікавай прамой.
і вы-явіце іх на
лікавай прамой.
1.4.
Зададзены мноствы ![]() ,
, ![]() ,
, ![]() .
Знайдзіце:
1)
.
Знайдзіце:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
1.5.
Няхай ![]() ,
, ![]() . Знайдзіце: 1)
. Знайдзіце: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
1.6.
Няхай А –найбольшае ваколле пункта ![]() , у якім праўдзіцца ня-роўнасць х2
– 5х + 4 < 0; В – найбольшае ваколле
пункта
, у якім праўдзіцца ня-роўнасць х2
– 5х + 4 < 0; В – найбольшае ваколле
пункта ![]() , у якім
, у якім
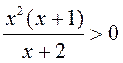 .
Знайдзіце : 1)
.
Знайдзіце : 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
1.7. У першым туры алімпіяды ўдзельнічалі 100 студэнтаў, з іх 70 чалавек атрымалі права ўдзельнічаць у другім туры алімпіяды па фізіцы, 45 – па матэматыцы. Вядома, што 23 чалавекі могуць браць удзел у другім туры і па фізіцы, і па матэматыцы. Колькі студэнтаў не дапушчана да другога туру ні па фізіцы, ні па матэматыцы?
1.8. Няхай А – падмноства мноства натуральных лікаў. Кожны элемент мноства А ёсць лік, які кратны ці ліку 2, ці 3, ці 5. Знайдзіце колькасць элементаў у мностве А, калі сярод іх ёсць: 70 лікаў, якія кратныя 2; 60 лікаў, кратных 3; 80 лікаў, кратных 5; 32 лікі, кратныя 6; 35 лікаў, кратных 10; 38 лікаў, кратных 15; 20 лікаў, кратных 30.
1.9. Сярод абітурыентаў, якія паступілі на фізічны факультэт універсітэта, адзнаку “дзевяць” атрымалі: па матэматыцы – 48 чалавек; па фізіцы – 37; па беларускай мове 42; па матэматыцы ці фізіцы – 75; па матэматыцы ці беларускай мове – 76; па фізіцы ці беларускай мове – 66; па ўсіх трох дысцыплінах – 4. Высветліце: 1) колькі абітурыентаў атрымалі хаця б адну дзевятку; 2) колькі чалавек атрымалі толькі адну дзевятку.
1.10. Вылічыце: 1) 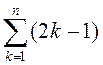 ; 2)
; 2) ![]() ; 3)
; 3) 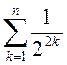 ; 4)
; 4) 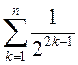 .
.
1.11. Вылічыце: 1) 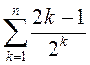 ; 2)
; 2) 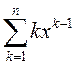 .
.
1.12. Вылічыце 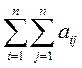 , калі:
1)
, калі:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
1.13. Вылічыце: 1)  ; 2)
; 2) 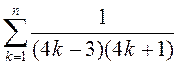 ;
3)
;
3) 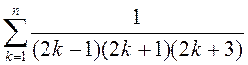 ; 4)
; 4) 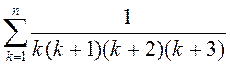 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.