Определение, формы представления графов. Матрица смежности для орграфа. Цикл Эйлера и цикл Гамильтона, страница 5

(" х_iÎХ) [Г(х_i) = Г₁(х_i) È Г₂(х_i)].

Рассмотрим пример. Пусть заданы графы G₁ и G₂, аналитические, геометрические и матричные представления которых изображены на рис. 5.1. и 5.2., соответственно.

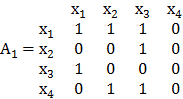Х₁={х₁, х₂, х₃, х₄}, Г₁(x₁)={х₁, х₂, х₃},

Г₁(x₂)={х₃},

Г₁(x₃)={х₁},

Г₁(x₄)={х₂,х₃}.

Х₂={х₁,х₃,х₅},

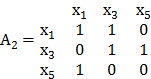Г₂(Х₁)={х₁ ,х₃},

Г₂(Х₃)={х₃,х₅},

Г₂(Х₃)={х₁},

Тогда  соответствующие представления графа G=G₁ÈG₂ имеют вид, изображенный на рис. 5.3.

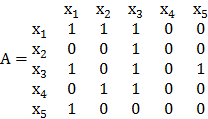Х = Х₁ È Х₂ = {х₁, х₂, х₃, х₄, х₅}

Г(х₁) = Г₁(х₁) È Г₂(х₁)={х₁, х₂, х₃},

Г(х₂) = {х₃},

Г(х₃) = Г₁₍х₃) È Г₂₍х₃)  = {х₁, х₃, х₅},

Г(х₄) = {х₂, х₃},

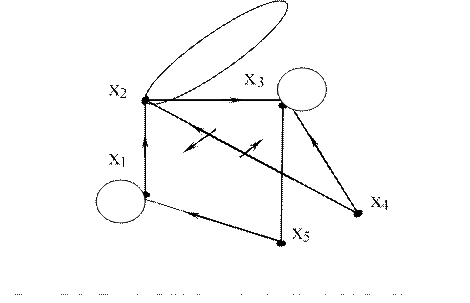Г(х₅) = {х₁}

При матричном представлении порядок исходных матриц можно сделать n x n, где n – мощность множества Х, путем добавления нулевых строк и столбцов, соответствующих тем вершинам, которые есть в объединении графов, но отсутствуют в исходных графах. Тогда любой элемент матрицы А оказывается дизъюнкцией соответствующих элементов в полученных таким способом матрицах.

В рассмотренном примере порядок исходных матриц следует сделать 5 х 5 путем добавления в матрицу А₁ нулевых строки и столбца, соответствующих вершине х₅ и путем добавления  в матрицу А₂ нулевых строк и столбцов, соответствующих вершинам х₂ и х₄ так, как это показано на рис. 5.4.

Операцию объединения можно распространить и на большее число графов. При этом объединяются как множества вершин, так и множества исходных ребер.

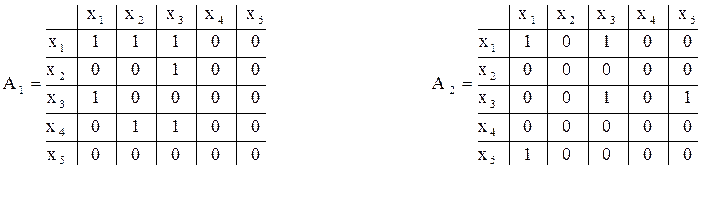5.2. Пересечение графов.

Пересечение G(Х, Г) графов G₁ (Х₁, Г₁) и G₂ (Х₂, Г₂), записываемое как

G(X, Г) = G₁ (X₁, Г₁ ) ∩ G₂ (X₂, Г₂), осуществляется по следующим правилам: 1) вершинами графа G является пересечение множеств вершин исходных графов: Х = Х₁ ∩ Х₂ ; 2) отображение для каждой вершины графа G получают в результате пересечения отображений этой вершины в исходных графах:

" х_i Î Х [ Г(х_i ) = Г₁ (х_i ) ∩ Г₂ (х_i )].

Для графов G₁ и G₂, изображающих на рис. 5.1. и 5.2. граф – пересечение G (его аналитическая, геометрическая и матричная формы) представлен на рис. 5.5.

 

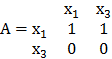G=G₁∩ G₂ ,

Х=х₁∩ х₂={х₁, х₃},

Г(х₁)={х₁, х₃},

Г(х₃)=Æ.

При нахождении пересечения в матричной форме порядок исходных матриц можно сделать m х m, где m – мощность множества Х=Х₁ Õ Х₂, путем вычеркивания строк и столбцов, соответствующих вершинам, не входящим в множество Х = Х₁ Õ Х₂. Тогда любой элемент матрицы А оказывается конъюнкциейсоответствующих элементов полученных таким способом матриц.

В рассмотренном примере эти матрицы имеют вид:

Операцию пересечения можно распространить и на большее число графов.

5.3.Вычитание графов

Вычитание G(Х,Г) графов G₁(Х_1, Г₁) и G₂ (Х₂, Г₂), записываемое как

G(Х, Г) = G₁(Х₁, Г₁) \ G₂(Х₂, Г₂),

Осуществляется по следующим правилам: 1) вершинами графа G являются вершины графа G1 за исключением вершин, общих для исходных графов: Х=Х1 Х2; 2) отображением для каждой вершины графа G является пересечение множества вершин этого графа и отображениея той же вершины в графе G₁: " х_i Î х [Г(х_i ) = Х ∩ Г₁(х_i )].

Для рассмотренного выше примера аналитическое, геометрическое и матричное представление графа G(Х, Г) = G₁(Х₁, Г₁) \ G₂(Х₂, Г₂) изображены на рис. 5.6.

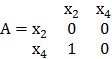Х = х₁ х₂  = {х₂, х₄}

Г(х₂) = Х ∩ Г₁(х₂) = {х₂, х₄} ∩ {х₃} = Æ

Г(х₄) = Х ∩ Г₁(х₄) = {х₂, х₄} ∩ {х₂,х₃} = {х₂}

Упражнения

5.1. Графы G₁  и G₂ заданы своими матрицами смежности А₁ А₂. Найти их объединения, пересечение и разность и представить результаты в аналитической, геометрической и матричной формах.

6. Деревья

Одним из наиболее важных и часто используемых понятий теории графов является дерево. Дадим определение неориентированного и ориенBЀированного деревьев.