Определение, формы представления графов. Матрица смежности для орграфа. Цикл Эйлера и цикл Гамильтона, страница 4

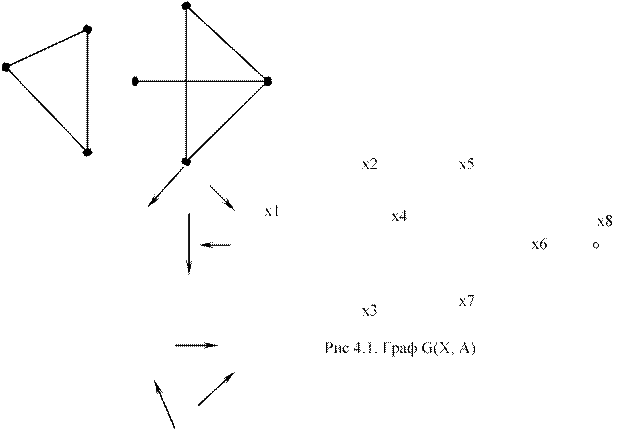
Х1 = {х1, х2, х3, х4};

Х2 = {х5, х6, х7};

Х3 = {х8}

Х = Х1 ( Х2 ( Х3.

Ранг R графа G определяется как разность числа вершин n графа и числа компонент связности р, т.е.

R(G) = n - p.

Для графа на рис. 4.1. R(G)=5

Изоморфные графы. При геометрическом изображении графа существует большая свобода в размещении вершин графа в пространстве, т.е. один и тот же граф может иметь различное геометрическое представление.

Графы G и G( называются изоморфными, если они имеют одинаковое число вершин и если каждой паре вершин, соединенных ребром (дугой), в одном графе соответствует такая же пара вершин, соединенных ребром (дугой той же ориентации) в другом графе. Все изоморфные графы имеют одни и те же свойства, а различные их изо-бражения помогают иногда выявить некоторые свойства, например, планарность графа.

На рис. 4.2. (а), (б), (в) изображены изоморфные графы  G, G( и G((. В графе G( на рис. 4.2. (б) выделен в виде самонепересекающейся цепи гамильтонов цикл {х1, х3, х2, x7, x5, х6, х4, х1); рис. 4.2. (в) показывает, что граф G(( планарный (плоский) и, следовательно, графы G и G( тоже плоские.

Рис. 4.2.

Граф G (Х, А) называют плоским или планарным, если он может быть изображен на плоскости так, что все его ребра пересекаются только в вершинах Х графа.

При использовании графа в качестве модели принципиальной электрической схемы, решая вопрос о возможности реализации схемы с помощью печатного монтажа, важно знать, является ли граф плоским и , если да, то как получить его изображение на плоскости без пересечения ребер.

Критерий, позволяющий указать общие условия существования плоского графа весьма сложен для практического использования. Здесь мы рассмотрим частные случаи.

Пусть граф G (Х, А) с n  вершинами имеет гамильтонов цикл и получено его изображение, в котором ребра гамильтонова цикла не пересеваются, как на рис. 4.2. (б). Тогда во внутренней и внешней областях по отношению к циклу гамильтона можно провести без пересечений не более (n-3) ребер(1]. Cледовательно,  максимальное число ребер (некратных) у плоского графа :

mmax = n + (n - 3) + (n - 3) = 3(n - 2).

Кроме того, что если число некратных ребер графа m ( n + 2 то такой граф заведомо плоский .(1(

Числом планарности графа называется минимальн>Ѐе число ребер, которое необходимо удалить из графа для получения его плоского изображения. Например, для графа на рис. 4.3. число планарности равно единице, т.к. для получения его плоского изображения необходимо удалить, как это видно из рисунка, одно ребро (х1, х4).

               Минимальное число плоских суграфов, котрое можно выделить в графе, называют толщиной графа. Толщина графа определяет минимальное число плоскостей (слоев), на коором может быть размещен граф без пересечения ребер в каждом слое.

Упражнения

4.1 Будут ли одинаковыми матрицы смежности и индиденций для графов G, G( и G(( на рис.4.2.(

4.2. Чему равно число ребер в полном графе(

4.3. Является ли плоским граф, который может быть изображен проволочной моделью куба(

4.4. Привести примеры графов с шестью вершинами, не являющихся плоскими.

4.5. Показать чему равно число планарности полного графа с пятью вершинами.

4.6. Являются ли графы G1и G2 на рис .4.4. изоморфными(

4.7. Определить число планарности и толщину графов G1 и G2

на рис. 4.4.

4.8. Определить толщину графа с мощностью множества вершин от 1 до 10, т.е. (х(=1 ( 10

5. Операции над графами.

5.1 Объединения графов

Объединение G(Х, Г) графов G1(Х1 ,Г1) и G2 (Х2, Г2) записываемое как  G(Х, Г)=G1(Х1, Г₁) È G₂(Х₂, Г₂), осуществляется по следующим правилам: 1) вершинами графа G(Х, Г) является объединение множеств вершин исходных графов: Х = Х₁ È Х₂; 2) отображение для каждой вер-шины графа G получают путем объединения отбражений этой вершины для исходных графов