В результате получаем матрицу вида:
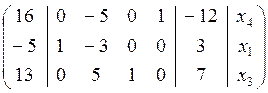
таким образом ![]() ,
,![]() ,
,![]() являются
базисными, а переменная
являются
базисными, а переменная ![]() является
свободной.
является
свободной.
Пусть свободная переменная ![]() .
Получаем значение базисных переменных:
.
Получаем значение базисных переменных:
х1=-3+3![]()
х3=7-5![]()
х4=-12+5![]()
Таким образом, система имеет бесконечное множество
решений, которые получаются, задавая ![]() различные
значения.
различные
значения.
х1=-3+3![]() ; х2=
; х2=![]() ; х3=7-5
; х3=7-5![]() ; х4=-12+5
; х4=-12+5![]() .
.
7.3 Решение систем линейных уравнений по формулам Крамера.
Этот метод решения используется при решении систем линейных уравнений, когда количество неизвестных равно числу уравнений и определитель основной матрицы системы не равен нулю.
Приведём здесь формулы Крамера для случая n=3, то есть для системы трёх уравнений с тремя неизвестными.
Рассмотрим систему:
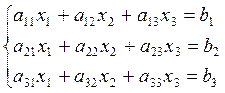
основная матрица системы А
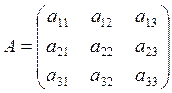
Вычисляем определитель основной матрицы системы,
обозначив его ![]() :
:
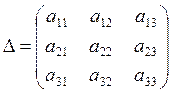
если определитель ![]() ,
то система имеет единственное решение и для нахождения неизвестных х1,
х2, х3 необходимо найти ещё три
определителя, которые получаются заменой столбцов определителей основной
матрицы, столбцами свободных членов.
,
то система имеет единственное решение и для нахождения неизвестных х1,
х2, х3 необходимо найти ещё три
определителя, которые получаются заменой столбцов определителей основной
матрицы, столбцами свободных членов.
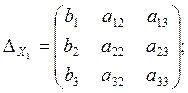
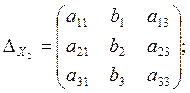
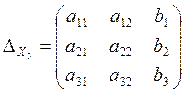
вычислив эти определители получаем формулы Крамера, для нахождения неизвестных х1, х2, х3.
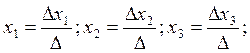
7.4 Решение систем линейных уравнений матричным способом.
Этот метод, как и предыдущий, используется для решения квадратичных систем, то есть систем имеющих одинаковое число уравнений и неизвестных. Причём для применения этого метода основная матрица системы должна быть невырожденной, и таким образом для нее существует обратная матрица. Рассмотрим применение этого метода на примере системы трёх уравнений с тремя неизвестными.
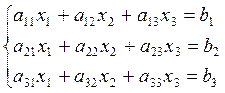
Для данной системы уравнений имеем основную матрицу системы, матрицу столбец свободных членов и матрицу столбец неизвестных:
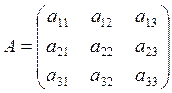 ;
; 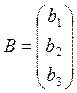 ;
; 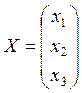 ;
;
тогда система уравнений в матричном виде имеет вид:
![]()
так как матрица А по условию является
невырожденной то для неё существует обратная матрица А-1.
Домножим матричное уравнение на матрицу А-1 слева, получим. ![]()
Произведение ![]() ,
так как ЕХ=Х окончательно получим Х=А-1В.
,
так как ЕХ=Х окончательно получим Х=А-1В.
Таким образом, для решения системы матричным методом, необходимо найти обратную матрицу основной матрицы системы А и затем, умножив ее на матрицу столбец получим матрицу столбец неизвестных.
Рассмотрим примеры, связанные с темой главы 7.
Пример 1:
Решить систему уравнений тремя методами:
1. Методом Гаусса;
2. По формулам Крамера;
3. Матричным методом.
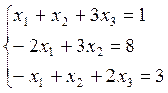
Решение методом Гаусса:
Для использования этого метода выпишем расширенную матрицу системы, включив в нее столбец контрольных сумм КΣ и столбец в котором указываем базисные переменные:
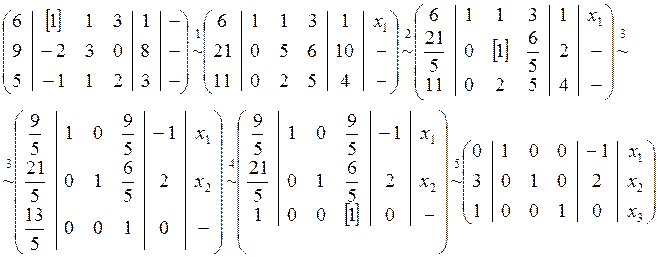
В конечной матрице содержатся только базисные неизвестные, поэтому система имеет единственное решение.
х1=-1; х2=2; х3=0.
Приведём описание действий, которые были выполнены в процессе элементарных преобразований.
1. В качестве разрешающего элемента выбран элемент, стоящий в первой строке и первом столбце. С помощью элементарных преобразований в первом столбце получены нулевые элементы во второй и третьей строках. В результате этих преобразований переменная х1 стала базисной.
2. Элементы второй строки умножаем на ![]() .
.
3. В качестве разрешающего элемента выберем элемент второй строки расположенный во втором столбце. С помощью элементарных преобразований во втором столбце получаем нулевые элементы в первой и третьей строках. В результате этих преобразований переменная х2 становится базисной.
4. Элементы третьей строки умножаем на ![]() .
.
5. В качестве разрешающего элемента выбираем элемент третьей строки стоящий в третьем столбце. С помощью элементарных преобразований в третьем столбце получены нулевые элементы в первой и второй строках.
Решение системы по формулам Крамера:
Для использования формул Крамера, необходимо выписать четыре определителя третьего порядка.
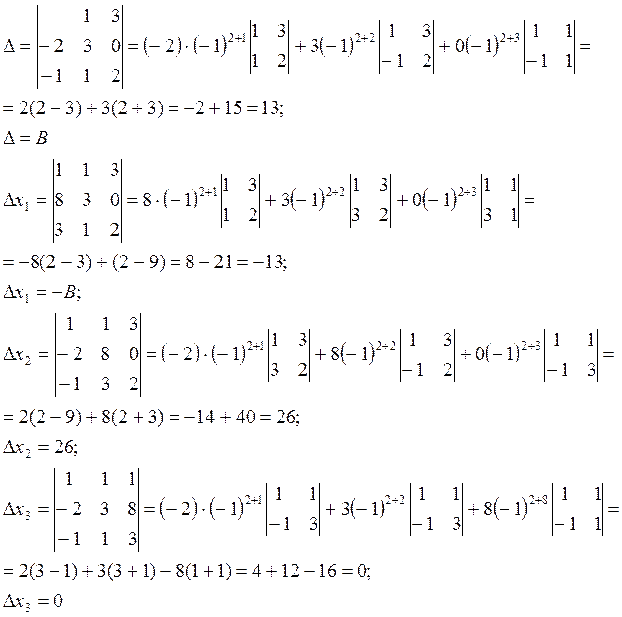
тогда используя формулы Крамера находим х1, х2, х3:
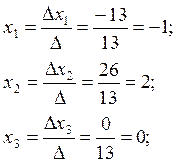
Решение системы матричным методом:
Для решения системы матричным методом выпишем основную матрицу системы, матрицу столбец неизвестных и матрицу столбец свободных членов.
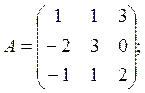
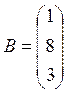 ;
; 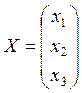
Для использования матричного метода необходимо найти обратную матрицы А-1. Вычислим сначала определитель основной матрицы.
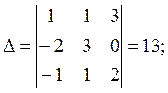 (Смотри
предыдущий пример)
(Смотри
предыдущий пример)
![]()
Матрица невырожденная, следовательно, существует обратная матрица.
Найдём алгебраические дополнения ко всем элементам определителя основной матрицы:
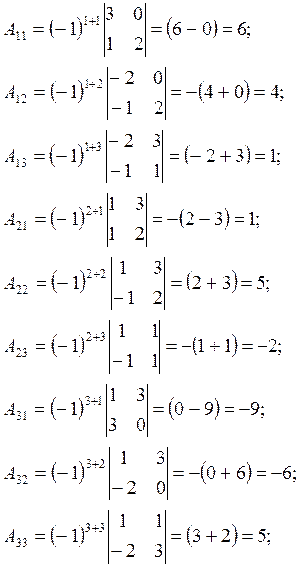
тогда обратная матрица имеет вид:
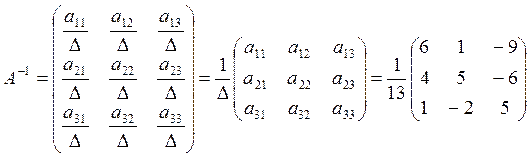
найдём матрицу Х.
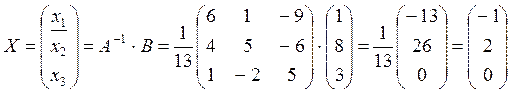
таким образом х1=-1; х2=2; х3=0.
Задачи для самостоятельного решения
1. Решить систему по формулам Крамера и матричным способом.
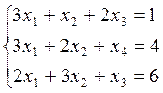
2. Решить систему уравнений методом Жордана Гаусса.
a.
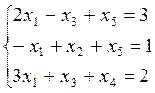
b.
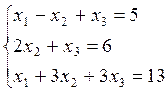
c.
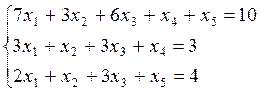
d.
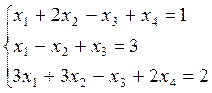
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.