Разложение обратных тригонометрических функций в степенные ряды
|
Разложить в ряд Маклорена функцию |
y = arcsin x |
Применим интегрирование степенных рядов.
1
Рассмотрим функцию f (x) =;
![]() 1−
x2
1−
x2
![]() −
Представим
f (х) в виде f ( )x
=
(1+
(−
x2
))
и воспользуемся известным разложением бинома
−
Представим
f (х) в виде f ( )x
=
(1+
(−
x2
))
и воспользуемся известным разложением бинома
![]() (1+t)m
=1+
mt
+
m(m−1)t
2
+
(1+t)m
=1+
mt
+
m(m−1)t
2
+
![]() m(m
−1)(m−
2)t3
+K+
m(m
−1)(m−
2)t3
+K+
1! 2! 3!
m(m −1)(m− 2)K(m −n +1) n
+ ![]() t +K,−1<
t
<1
t +K,−1<
t
<1
n!
Полагая теперь m =
−![]() , t =−x2,
получим
, t =−x2,
получим
⎛ 1⎞ ⎛ 1⎞⎛ 3⎞
⎜− ![]() ⎟ ⎜−
⎟ ⎜− ![]() ⎟⎜−
⎟⎜− ![]() ⎟
⎟
f ( )x =1+ ⎝ 2⎠(−x2 )+ ⎝ 2⎠⎝ 2⎠ (− x2 )2 +
1! 2!
⎛
1⎞⎛
3⎞⎛
5⎞(
2
)3
⎛
1⎞⎛
3⎞⎛
5⎞
⎛1
⎞
⎜− ⎟⎜− ⎟⎜− ⎟ − x ⎜− ![]() ⎟⎜−
⎟⎜−
![]() ⎟⎜−
⎟⎜− ![]() ⎟K⎜
⎟K⎜
![]() − n
+1⎟
− n
+1⎟
![]() ⎝ 2⎠⎝ 2⎠⎝ 2⎠ ⎝ 2⎠⎝ 2⎠⎝ 2⎠ ⎝2 ⎠( 2
)n
⎝ 2⎠⎝ 2⎠⎝ 2⎠ ⎝ 2⎠⎝ 2⎠⎝ 2⎠ ⎝2 ⎠( 2
)n
+..+ − x 3! n!
или, произведя упрощения, получаем
![]()
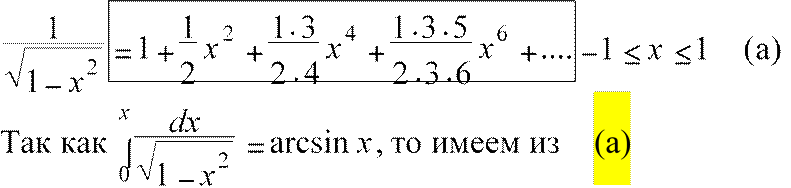
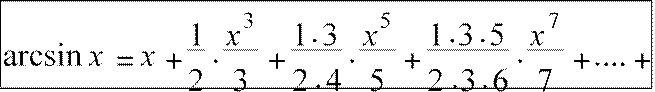
|
Разложить в ряд Маклорена функцию |
y = arctgx |
Можно разложить, вычисляя коэффициенты Тейлора.
Применим интегрирование степенных рядов.
Рассмотрим
геометрическую прогрессию (в которой вместо x возьмем -x2)
1−
x2
+
x4
−
x6
+...+...
=
![]() 1
при (| x |<1)
1
при (| x |<1)
2
1+ x
Интегрируем этот ряд
 dx.
Отсюда 2
dx.
Отсюда 2
0 0
1+
x
x  ,
,
Ряд сходится при −1≤ x ≤1 !
|
5 2n −1 |
Степенные ряды применяются для вычисления с заданной точностью значений функций; для приближенного вычисления определенных интегралов и для решения других задач, в частности, при интегрировании дифференциальных уравнений.
|
Задача |
: вычислить число π с точностью ……. |
При x =1 из (*) имеем еще один способ вычисления числа π :
|
Задача |
: вычислить число e с точностью 0,0001 |

 (−1)n−1
(−1)n−1
arctg1= =1− +...+ ![]() +...
+...
2n −1
2 n
Из формулы ex =1+
x
+
![]() x +...+
x +...+
![]() x +...
при x =1
x +...
при x =1
2! n!
получаем (знакоположительный) ряд
|
1 1 e
=
2+ 2! n! |
Так как 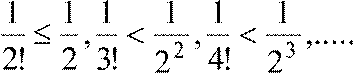 ,
то
,
то
1 1 1 1 1
![]() e =
2+
e =
2+ ![]() +...+
+...+ ![]() +...<
2+ + + +...
=
2+ =
2+1=
3
+...<
2+ + + +...
=
2+ =
2+1=
3
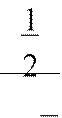 2! n! 2 22 23 1−
1
2! n! 2 22 23 1−
1
2
или 2 < e < 3.
Тогда при x =1 остаточный член в форме Лагранжа
e1 3
![]() удовлетворяет
неравенству | Rn(x) |≤ <
(n +1)! (n +1)!
Найдем требуемое n из условия Rn <
0,0001
или
удовлетворяет
неравенству | Rn(x) |≤ <
(n +1)! (n +1)!
Найдем требуемое n из условия Rn <
0,0001
или
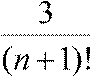 <
0,0001.
Отсюда n
<
0,0001.
Отсюда n 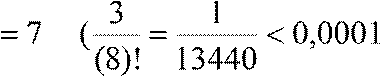 ).
).
Итак  e
e
|
1 Вычислить приближенно с точностью до
|
![]() 0,0001
.
0,0001
.
1 −
Поскольку = e, то из известного разложения
![]() 4
e
4
e
x x2 x3 xn
![]()
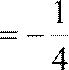
![]() e =1+
x
+ + +K+ +K
2! 3! n!
e =1+
x
+ + +K+ +K
2! 3! n!
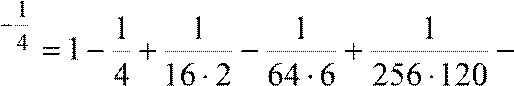 при
x, получаем
при
x, получаем
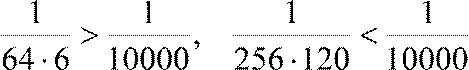 eK
.
eK
.
Поскольку , то для достижения заданной точности достаточно четырех первых членов разложения:
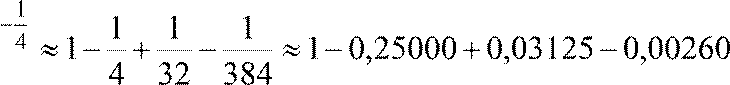
e
|
|
≈ 0,77865 ≈ 0,7787
0,001 .
1
![]()
![]()
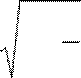

![]()
![]() 3 9 =
2⋅3
9
=
2⋅3
1+
1
=
2⎜⎛1+
1⎞⎟
3 Здесь m =
1,x
=
1
3 9 =
2⋅3
9
=
2⋅3
1+
1
=
2⎜⎛1+
1⎞⎟
3 Здесь m =
1,x
=
1
8 8 ⎝ 8⎠ 3 8
9
 =
2⎜1+ ⎟ =
2⋅(1+ ⋅ + ⋅(
−1)(
) ⋅ +...
=
=
2⎜1+ ⎟ =
2⋅(1+ ⋅ + ⋅(
−1)(
) ⋅ +...
=
⎝ 8⎠ 3 8 3 3 8 2!
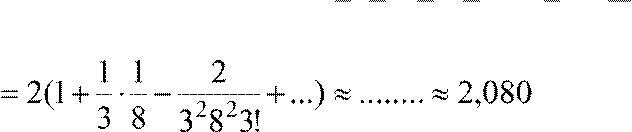
![]()
|
Задача |
: вычислить число cos50 с точностью 0,0001 |
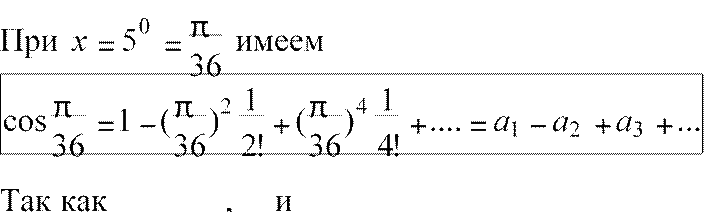
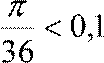

a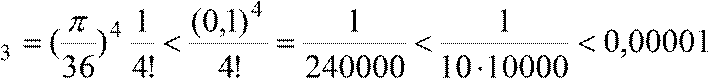 то cos50
≈
a1
−
a2
≈1−0,0038
=
0,9962
то cos50
≈
a1
−
a2
≈1−0,0038
=
0,9962
|
Задача |
2ex − 2− 2x − x2 : Найти lim x→0 x −sin x |
x2 x3 x4 2
=lim= x→0
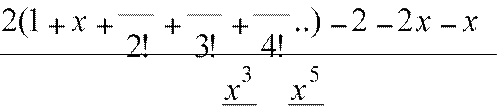 x
−(x
−
+ +..)
3! 5!
x
−(x
−
+ +..)
3! 5!
2x3 x4 2 x
+ +.... + +....
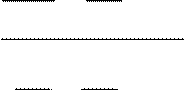
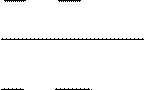 =
lim
3! 4! = lim 3! 4! =
2
x→0
x3 x5 x→0
1 x2
− +... − +...
=
lim
3! 4! = lim 3! 4! =
2
x→0
x3 x5 x→0
1 x2
− +... − +...
3! 5! 3! 5!
![]()
|
Задача |
1 sin x :Вычислить с точностью
до 0,0001 ∫ 0 x |
sin x
Неопределенный интеграл ∫ ![]() dx
относится к
dx
относится к
x
sin x
«неберущимся»
интегралам. Разложим ![]() в ряд x
в ряд x
sin x 1 ⎛ x3 x5 x7 ⎞ x2 x4 x6
![]()
![]()
![]() x =
x
⎜⎜⎝x
−
3!
+
5!
−
7!
+K⎟⎟⎠
=1−
3!
+
4!
−
6!
+K
x =
x
⎜⎜⎝x
−
3!
+
5!
−
7!
+K⎟⎟⎠
=1−
3!
+
4!
−
6!
+K
1 sin x 1⎛ x2 x4 x6 ⎞
![]() 0∫
0∫ ![]() dx
=
0∫⎜⎜⎝1−
3!
+
4!
−
6!
+K⎟⎟⎠dx
=
x
dx
=
0∫⎜⎜⎝1−
3!
+
4!
−
6!
+K⎟⎟⎠dx
=
x
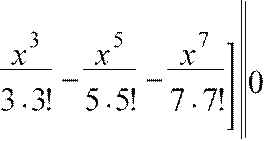 1
1
⎡+K =
⎢x −
⎣
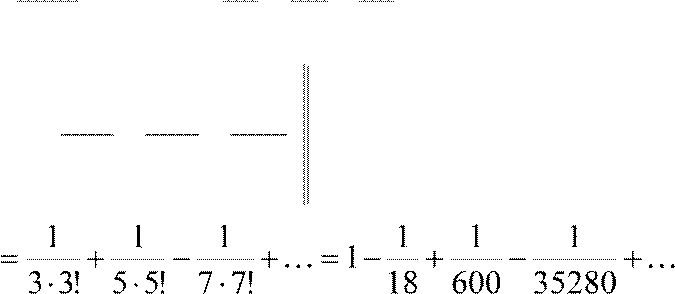 .
.
В правой части ряд Лейбница, поэтому
его остаток не превосходит по абсолютной величине первого отбрасываемого
члена. Так 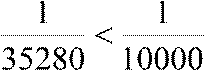 , то для вычисления интеграла с требуемой точностью
0,0001 достаточно взять три первых члена разложения:
, то для вычисления интеграла с требуемой точностью
0,0001 достаточно взять три первых члена разложения:
1 sin x 1 1
![]() ∫
∫ ![]() dx
=1− + ≈
0,9461.
dx
=1− + ≈
0,9461.
0 x 18 600
|
Задача |
: |
Вычислить 0 |
2 3 n n
![]() e−x
=1− x
+
x −
x
+...+
e−x
=1− x
+
x −
x
+...+ ![]() (−1)
x +... .
(−1)
x +... .
2! 3! n!
Интегрируя его почленно, получим:
![]()
![]() x 0,5 x2 x3 (−1)n
xn
x 0,5 x2 x3 (−1)n
xn
![]() dx=
∫ (1−
x
+ − +...+
dx=
∫ (1−
x
+ − +...+ ![]() +...)dx
=
+...)dx
=
0 2! 3! n!
![]()
![]()
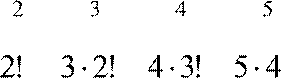 x
x x x (−1)n xn+10,5
=
(x
−
+ − + ..+
+...0
=
x
x x x (−1)n xn+10,5
=
(x
−
+ − + ..+
+...0
=
! (n +1)n!
(0,5)2 (0,5)3 (0,5)4 (−1)n0,5n+1
![]() = 0,5−
+ − +...+
= 0,5−
+ − +...+
![]() +....
. 2! 3⋅2!
4⋅3!
(n +1)n!
+....
. 2! 3⋅2!
4⋅3!
(n +1)n!
По признаку Лейбница остаток сходящегося знакочередующегося ряда не превосходит по абсолютной величине абсолютной величины первого отбрасываемого члена, поэтому
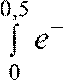
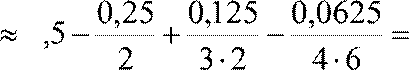 x
x
dx 0
0,5−1,125+ 0,0208−0,0026 =0,0182 ≈ 0,018.
Заданная точность обеспечена, так как первый отброшенный член удовлетворяет требуемому неравенству
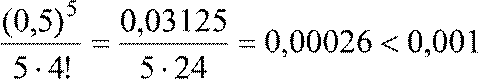 .
.

Решение будем искать в виде степенного ряда y(x) = a0 + a1 ⋅ x + a2 ⋅ x2 +...... (Р)
Из начальных условий при x = 0 можно определить коэффициенты a0 = 0,a1 =1.
(В противном случае они служат произвольными постоянными общего решения ДУ).
Дважды дифференцируя ряд (Р) и подставляя в ДУ, имеем (учтем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.