Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами

	Определение	Дифференциальное уравнение вида py′+ qy = f (x),            (1)                   константы,        f (x)—заданная                                   функция линейным неоднородным дифференциаль второго порядка с постоянными .
	y′′+ где p,q— называется ным уравнением коэффициентами

Как устроено общее решение ЛНДУ ?

Теорема  (структура общего решения ЛНДУ). 

Общее          решение         линейного                  неоднородного

дифференциального уравнения ЛНДУ (1) есть сумма y(x) = y*(x)+ y_общ(x)          (*)

некоторого частного решения y*(x) неоднородного ДУ (1) и общего решения      y_общ(x) = C₁y₁(x) +C₂y₂(x)

однородной части ДУ (1), т.е. решения  для ДУ вида                  y′′+ py′+ qy = 0.                        (**)

Здесь y₁(x), y₂(x) линейно независимые решения для ДУ (**),   а   C₁,C₂ —произвольные постоянные.

Как искать частное решение неоднородного ДУ?

Укажем для специального вида правой части f (x)!!

1.     Пусть  

f(x)=P_n(x)≡a₀xⁿ+a₁xⁿ⁻¹+...+a_n−1x+a_n

а) Предположим, что число λ = 0 не является корнем характеристического уравнения          λ² + pλ + q = 0Тогда частное решение для неоднородного уравнения ищем тоже  в виде многочлена той же степени, (но с неизвестными пока коэффициентами): y*(x)=Rn(x)≡b0xn+b1xn−1+...+bn−1x+bn  (а1)

Подставим (а1) в ДУ (1):⇒

R_n′′(x)+ pR_n′ (x) + qR_n(x) ≡ P_n(x) для ∀x         (в1)

б) Пусть число λ = 0  является корнем (однократным !)  характеристического уравнения          λ² + pλ + q = 0(в этом случае оно имеет вид λ(λ + p) = 0)!

Тогда частное решение для неоднородного уравнения ищем   в виде 

                        y*(x)=x⋅Rn(x)                              (а2)

в) Пусть число λ= 0  является корнем (двухкратным !)  характеристического уравнения          ^λ2 + pλ+ q = 0

(в этом случае оно имеет вид λ² = 0)!

Тогда частное решение для неоднородного уравнения ищем   в виде 

                        y*(x)=x2⋅Rn(x)                              (а3)

Пример.

Найти общее решение дифференциального уравнения   y′′ − 2y′ + 2y = x².

Решение. 1)Ищем общее решение для y′′− 2y′+ 2y = 0. 

Характеристическое уравнение: λ² − 2λ+ 2 = 0,

D = 4 −8 = −4 = 4i², λ_1,2 = ^{2 ± 2i} =1± i, α=1, β=1, 

2

Значит, общее решение однородного уравнения есть

y_общ = e^x(C₁sin x +C₂ cosx).

2) Для нахождения частного решения неоднородного уравнения используем специальный вид правой части 

P_n(x) = x², n = 2.

Так как среди корней характеристического уравнения нет  λ= 0, то множители x и x² отсутствуют, значит, ищем частное решение y^∗ в виде многочлена второй степени с неопределенными коэффициентами             y^∗ = ax² + bx + c,    y^′∗ = 2ax + b,       y′^′∗ = 2a. 

Подставляем y^∗, y^′∗, y′^′∗ в исходное уравнение

y′′ − 2y′ + 2y = x²

Имеем

2a − 4ax − 2b + 2ax² + 2bx + 2c = x²;

x²(2a) + x(−4a + 2b) + 2a − 2b + 2c = x².

x2 :⎧2a =1, x1 :⎪⎨− 4a + 2b = 0,

⇔

⎧a =1 2, ⎪ ⎨ b =1,

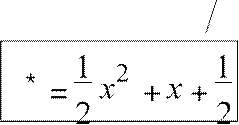x⁰ :^⎪_⎩2a − 2b + 2c = 0.                     ^⎪⎩c =1 2.

Итак, частное решение y                              . 

Следовательно, общее решение  неоднородного  ДУ  есть 

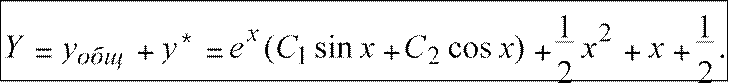
2.    Пусть  правая часть имеет вид

f(x)=e^kx⋅P_n(x)≡e^kx⋅(a₀xⁿ+a₁xⁿ⁻¹+...+a_n−₁x+a_n)

Важную роль играет взаимодействие корней характеристического уравнения с правой частью!!!

Пусть λ_i,i =1,2 — корни характеристического уравнения                 λ² + pλ+ q = 0 Возможны случаи: а)   k ≠ ^λ_i

kx Тогда частное решение ищем в виде  y*(x)=e ⋅^R_n(x) где R_n(x)— многочлен n-ой степени с неизвестными коэффициентами.

б)   число k является простым корнем (кратности один) характеристического уравнения,  т.е.k =^λ₁  или   k =^λ₂

Частное решение ищем в виде     y*(x)=x⋅^ekx⋅^R_n(x) где R_n(x)— многочлен n-ой степени с неизвестными коэффициентами.

в)  число k является двукратным  корнем характеристического уравнения, т.е.k =^λ₁ =^λ₂ =λ

2 kx

Частное решение ищем в виде     y*(x)=x ⋅e ⋅^R_n(x) где R_n(x)— многочлен n-ой степени с неизвестными коэффициентами.

Пример.

Найти общее решение дифференциального уравнения                 y′′ − 2y′ + y = xe^x.

Решение. Характеристическое уравнение имеет вид             λ² − 2λ+1= 0,    (λ−1)² = 0,     λ₁ = λ₂ =1.

Значит, общее решение   есть      y = (C₁ + C₂x)e^x. 

Так как правая часть имеет вид xe^1⋅x и k =1 совпадает