Другие предметы \ Математический анализ

Приближенные методы решения задач математической физики. Методы коллокации, Ритца, Галеркина, конечных элементов, страница 4

Ограничиваясь тремя базисными функциями, ищем решение в виде суммы

и) (с) = С1Р1 (с) + С2Р2 (г) + Сзрз(с), где и 92 - соответствующие функции- П крышки П (15):

91 (с)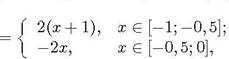

92 (с)

Для получения коэффициентов (31, (32, Сз составляем линейную алгебраическую систему

                 А11 С1 + А1202          з Сз

(31 + А22 (32 + А23 С3

82,

(24)

Аз 1               А 32 (32 + А 33 С3

d3.

Обращаясь к формулам (20) - (22), (17), имеем:

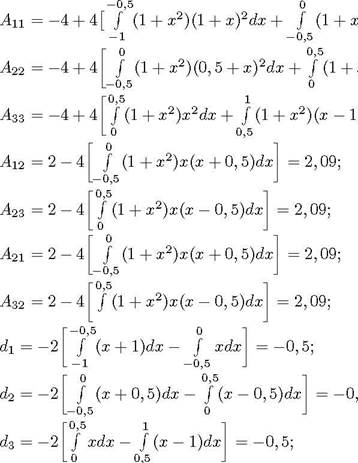(1 c2 )c 2 dcз, 575;

                                        — 0, 5) 2 dc            з, 658,


                              — 1) 2 dc       з, 575,

Подставляем эти числа в систему (24): з, 575 2,9

      2, 09          з, 658       2, 09

          2, 09                з, 575

Решая эту систему, находим ст = 0,662 С) = о 893, СЗ = СЧ.

Таким образом, приближенное решение из (с) есть из(с) О,  рз(с)) О, 89392(г).

1.2 Методы сплайн- коллокации.

Пусть требуется найти решение краевой задачи

             72,              (2)

1.2.1 1. Использование кубического сплайна

Введем на отрезке [а,Ьј неравномерную сетку Д : а и будем искать приближенное решение в виде кубического сплайна S(c) класса С) с узлами на сетке Д

Потребуем, чтобы сплайн S(c) удовлетворял уравнению (1) в точках ск [а, Ь], К = 0 ... п (условия коллокации), и краевым условиям (2):

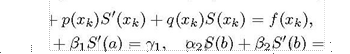
   LS(Tk)            (ск.)                                                                           К = 0 ...з П,        (з)

(4)

Пусть р(г) 0. Обозначим S(Ck) ик. , (ск) Мк Сплайн S(c) на отрезке гк. +1] определяется при этом формулой

S(c)

где t = (с — Отсюда

Неизвестные моменты Мк во внутренних узлах сетки удовлетворяют системе уравнении где ЏК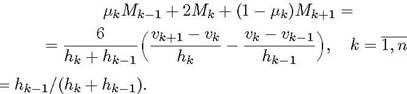

Из (3) имеем

                  Мк                 = Л., К = О...п.

Подставим Мк .fk              П. в соотношение (6) и получим:

Так как

то подставив в краевые условия (4), будем иметь

1

 01 ho —                                                                                     q1h0) = 71ho                ,B1h3 (2 .fo Л),

6

(8)

           1                                         1

       vn-1F2 (—1    6hn—1 ЧП —1              02hn_1 + ф (1З hn—1Qnj

               72hn-1 — -F2hn-1(fn-1 + 2fn).                             (9)

Уравнения (7)-(9) образуют разностную схему для решения задачи.

Методом прогонки из системы (7)-(9) вычисляются И., К 0, п. Определяют затем величины Мк и получают приближенное решение задачи

(1)-(2) в виде кубического сплайна S(c).

Пример 1. Методом конечных элементов решить краевую задачу [1]

            И.              (1 с 2 и 1 = 0; и(—1)

Решение. Вводим на отрезке [-1,1] равномерную сетку ск = kh с шагом 0,5.

Тогда систему линейных алгебраических уравнений (7) - (9) можно записать в следующем виде:

                 h2

(1 + —n-1)t'k-1

                    4fk Л.+1),       к = 1,2, з

6

или во внутренних узлах имеем: 2h2  h2  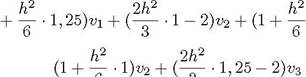      h2

h2

    (1                                                               . 1, 25)V36

6

h2

6

                6                      з                                          6

Решая данную систему методом прогонки, получаем:о, 6577 о, 8912.

1.2.2 П. Использование В-сплайнов

Решение задачи (1)-(2) ищется в виде разложения по базису из нормализованных кубических В-сплайнов:

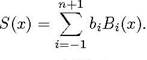                                                                  (10)

Чтобы все базисные функции в (10) были определены, сетка Д дополнятся тремя узлами в начале и в конце построенной сетки. Они выбираются так, чтобы выполнялись условия

Подставляя (10) в (3), получаем

bkLBk(Tk) + (ск) = Л,

Если учесть выражения для узловых значений В-сплайна и его производных, то эти уравнения можно записать в виде

              Ьк_1Ак ЬКСК  = РК, К =О...п                              (12)

где

               (13)

Из уравнений (4) с учетом условий (11) получаем

                                       (14)

где

01ho — 3931,

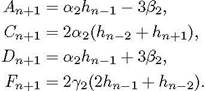
       201        111):

Скачать файл