Проектирование реконструкции плана существующего пути в едином комплексе проектирования второго пути, страница 4

b  – смещение тангенса изменяемой кривой.

Предварительно решается вспомогательная задача по определению расстояний между центрами кривых (существующими и проектируемыми) L_с  и L_пр, для чего определяются величины углов между направлениями прямых вставок и направлениями линий, соединяющих центры кривых:

- между существующими кривыми:

tg b1 = (R2 – R1)/dc;	(4.1)
Lс = dc /cos b1;	(4.2)

- между проектируемой и существующей кривыми:

tg b2 = (R2 – Rпр)/dпр;	(4.3)
Lпр = dпр /cos b2.	(4.4)

Из решения двух прямоугольных треугольников (см. рисунок 4.1) устанавливается величина b:

j1 = 90о – (b1 + a);	(4.5)
h1 = Lc cos j1;	(4.6)
h2 = h1 – (Rпр – R1);	(4.7)
cos j2 = h2/Lпр;	(4.8)
a2 = 90о – ( j2 + b2);	(4.9)
a1 = a– a2;	(4.10)
b = Lпр sin j2 – Lc sin j1,	(4.11)

где b₁, b₂, L_c, L_пр, j₁, j₂, h₁ и h₂ – вспомогательные величины.

Приведенный вывод дан для случая расчета, когда R₂>R_пр>R₁. При прочих условиях меняется расположение треугольников, однако принцип решения задачи не меняется.

4.2 Замена вставки и прилегающих участков кривых

одной новой кривой

Этот способ применяется обычно в случаях расположения второго пути снаружи кривой.

Последовательность расчета определяется решением геометрической задачи, представленной на рисунке 4.2.

В качестве исходных данных используются: радиусы существующих кривых R₁ и R₂, длина существующей прямой вставки d_с, радиус проектируемой кривой R_пр.

Для решения определяются:

a – угол сопрягающей кривой;

Δa₁ и Δa₂ – углы, отсекаемые от первой и второй кривых.

Искомые углы поворота определяются путем решения двух треугольников О¢О₁О₂ и О₁О₂О₃ (см. рисунок 4.2).

Элементы кривых определяются по следующим формулам:

- расстояние между центрами существующих кривых:

L = ;	(4.12)
В = R1 – R2;	(4.13)

- углы b₁ и b₂:

tgb1 = (R1 – R2)/dc;	(4.14)
b2 = 90о − b1.	(4.15)

Полупериметр S находится из косоугольного треугольника   О₁О₂О₃:

S = (A + Б +L)/2.

(4.16)

Рисунок  4.2 – Замена прямой Рисунок 4.1− Определение a1 и a2 и величины смещения тангенса b вставки круговой кривой

Вспомогательная величина

                             .                                  (4.17)                                      

Углы a, g₁ и g₂ определяются из следующих выражений:

tg  (a/2) = К/(S – L);                   tg  (g1/2) = К/(S – А);                   tg  (g2/2) = К/(S – Б).

(4.18) (4.19) (4.20)

Углы, отсекаемые от существующих кривых, определяются по формулам:

- от первой кривой

Δa1 = 180о – (g2 + b2);

(4.21)

- от второй кривой

Δa2= 180о – (g1 + b1 + 90о).

(4.22)

Правильность расчетов осуществляется проверкой:

Δa1 + Δa2  = a.

(4.23)

Если кривые небольшой длины разделены недостаточной прямой вставкой, то замену вставки и обеих прилегающих кривых проектируют в соответствии со схемой, приведенной на рисунке 4.3.

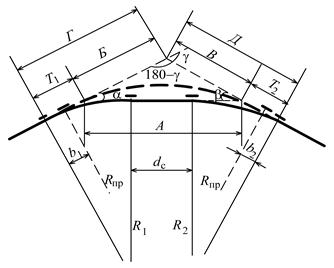
Рисунок  4.3 – Замена двух кривых и короткой вставки одной кривой

В этом случае используются следующие формулы:

Начало и конец новой круговой кривой определяются при помощи выражений:

b1 = Г – Тпр; b2 = Д – Tпр.

(4.30) (4.31)

Радиус новой кривой R_пр подбирается с учетом условия

Г ³ Тпр £ Д,

(4.32)

где Т_пр – тангенс кривой радиуса  R_пр.

Пример расчета увеличения прямой вставки указанным способом производится при исходных данных:

первая кривая                                                   вторая кривая

a₁ = 68^о58' ;                                                       a₂ = 29^о13';

R₁ = 615 м  ;                                                       R₂ = 675 м;

К₁ = 740,27 м;                                                    К₂ = 344,20 м;

Т₁ = 422,41 м;                                                    Т₂ = 175,93 м;

начало кривой – ПК61 + 35,76;                     начало кривой – ПК69 + 44,04;

конец кривой   – ПК68 + 76,03;                     конец кривой  –  ПК72 + 88,23.

Длина существующей прямой вставки d_с = 68,00 м. Существующая прямая вставка и прилегающие участки кривых заменяются одной новой кривой с  R_пр = 1500 м.

Аналитический расчет

Аналитический расчет основных элементов производится в соответствии с рисунком 4.4 с использованием формул (4.12)–(4.32).

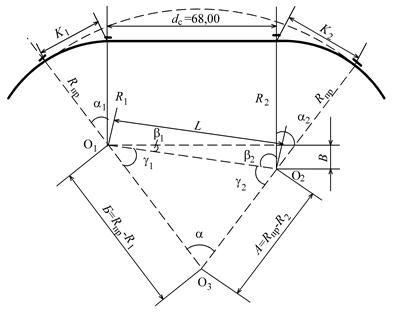
Рисунок 4.4 – К расчету основных элементов

   Определяются вспомогательные величины А, Б и В (см. рисунок 4.4)

А = R_пр – R₂ = 1500 – 675 = 825 м;

Б = R_пр – R₁ = 1500 – 615 = 885 м;

В = R₂ – R₁ = 675 – 615 = 60 м.

Расстояние между центрами кривых определяется по формуле (4.12):

м.

   Полупериметр определяется по формуле (4.16):

S = (825 + 885 + 90,69)/2 = 900,34 м.

Вспомогательная величина К определяется по формуле (4.17):

м.

Углы b₁, b₂, j₁, j₂ и j определяются по формулам (4.14)–(4.15) и (4.17)–(4.22):

tgb₁ = (675 – 615)/68 = 0,882353; b₁= 41^о25';

b₂ = 90^о – 41^о25' = 48^о35';

tg (j/2) = 32,23/(900,34 – 90,69) = 0,039807; j = 4^о34';

tg (g₁/2) = 32,23/(900,34 – 825) = 0,427794; g₁ = 46^о20';

tg (g₂/2) = 32,23/(900,34 – 885) = 2,101043; g₂= 129^о06';

Δa₁  = 180^о – 90^о – 41^о25' – 46^о20' = 2^о15';

Δa₂ = 180^о – 48^о35' – 129^о06'= 2^о19'.

Проверка производится по формуле (4.23):

a = Δa₁  + Δa₂  = 2^о15' + 2^о19' = 4^о34', т.е. проверка выполняется.

Величины углов остающихся кривых составят:

- первой кривой a₁ – j₁ =  68^о58' – 2^о15' = 66^о43';