Метод прямой капитализации дохода в двухскоростной модели DDM и CAPM, страница 2

Более того, известно, что единственное решение k* уравнения (20.7) может быть получено в этом случае методом последовательных приближений: k₀ – любое,

         

Пусть. Тогда . Функция F(.) убывает и  Отсюда следует, что функция

         

монотонно убывает и на концах интервала принимает значения разных знаков:

         

Следовательно в силу непрерывности и монотонности функции Ф(.) она обращается в ноль единственный раз на интервале  в некоторой точке k*, которая является решением уравнения (20.7). Это решение в силу монотонности функции Ф(.) может быть найдено методом деления отрезка пополам или простым подбором.

20.4. Аппроксимация основного уравнения

Аппроксимируем уравнение (20.1) линейным. Это приведет, как мы увидим, к квадратической аппроксимации уравнения (20.7).

Предположим, что

          ,       (20.13)                                                                               

равномерно по l. Тогда в линейном приближении по  справедлива формула:

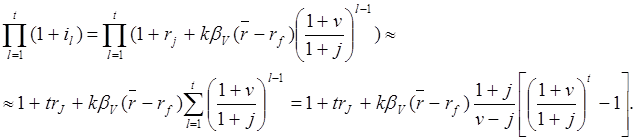(20.14)

С учетом (20.14) имеем с точностью до :

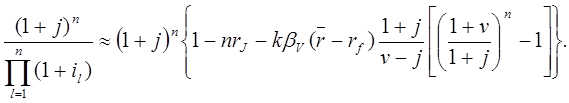   (20.15)                   

Аналогично справедливо равенство:

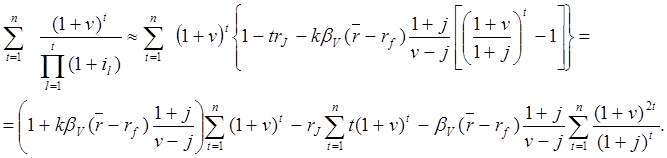(20.16)

Вторая сумма здесь вычисляется следующим образом:

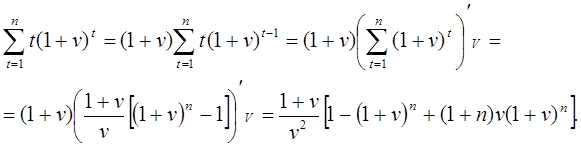 (20.17)                 

Подставляя (20.17) в (20.16) и вычисляя оставшиеся суммы, получим:

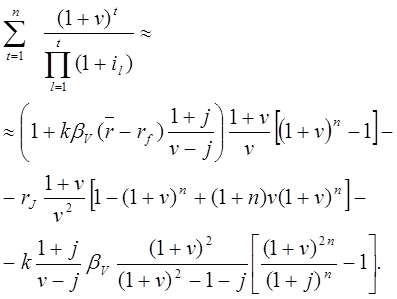                    (20.18)                      

Подставляя (20.15), (20.18) в (20.1), получим приближенную формулу:

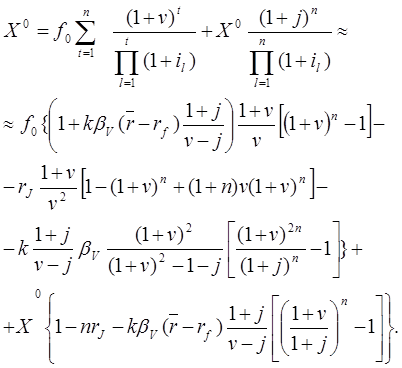 (20.19)                                           

Полученная формула в отличие от (20.1) является конечной. Уравнение (20.19) можно записать в виде (20.20):

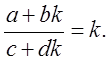                         (20.20)                                                                              

Здесь обозначено для краткости:

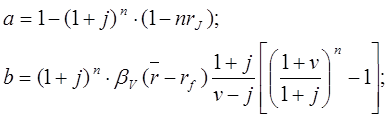   (20.21)                                               

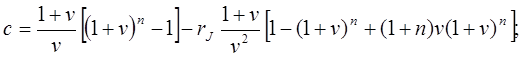        (20.22)                               

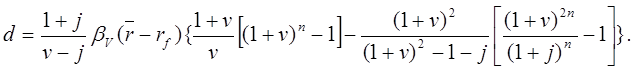 (20.23)                                                         

Левая часть (20.20) по смыслу аппроксимирует функцию F(.) в (20.7). Уравнение (20.20) является квадратическим уравнением относительно k и может быть решено с использованием «школьной» формулы. Необходимо помнить, что экономический смысл имеет только неотрицательное решение уравнения (20).

20.5. Числовой пример

Приведем числовой пример определения ставки капитализации для оценки бизнеса на основе примера описанного в главе 20. Напомним, что для этого была использована информация об индексе РТС и квартальная бухгалтерская отчетность предприятия (бухгалтерский баланс и отчет о прибылях и убытках) за 7 кварталов начиная с 1 января 2000г. до даты оценки 1 октября 2001г. Индекс РТС был известен с точностью до получаса, а бухгалтерская отчетность –– поквартально. В связи с эти периодом расчета был выбран квартал с тем, чтобы получить максимальный объем информации с начала 2000г. Начало отсчета было привязано к моменту, когда начался заметный подъем в российской экономике и, следовательно, можно было рассчитывать на стационарность рассматриваемых процессов ценообразования. Необходимые для расчета числовые характеристики были получены в [1]:

n=24;

Уравнение (20.20) с учетом формул (20.1)-(20.23) имеет вид:

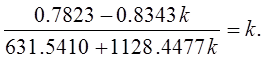
После преобразований оно приводится к квадратному уравнению:

         

Это уравнение имеет единственный положительный корень

         

В данном случае выполнено (20.11):

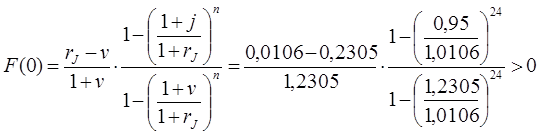
и .

Применяя алгоритм

         

при получим за 5 шагов решение  Сравнивая с раннее полученным решением в линейном приближении , видим, что точность последнего невысока. Таким образом, следует пользоваться методом последовательных приближений, основанном на принципе сжимающих отображений. Однако приближенная формула (20.19) оказывается полезной, так как ее правая часть дает конечное приближение оценке инвестиционной стоимости, полученной в главе 20.

Имея ставку капитализации, получим оценку стоимости бизнеса по формуле

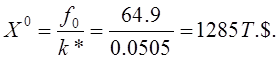
Этот результат близок к затратной (балансовой) стоимости бизнеса, которая составляла в рассматриваемом случае 1348т.$.

В заключение отметим, что настоящая глава является продолжением предыдущей главы по двухскоростной модели DDM и CAPM в части определении неизвестной ставки капитализации k непосредственно из основного уравнения (20.1). Сначала казалось, что этот путь бесперспективен, и полученное нелинейное уравнение нельзя корректно исследовать и, тем более, решить. Однако применение принципа сжимающих отображений позволило полностью решить поставленную задачу. В частности, удалось установить условия существования и единственности уравнения (20.7) и обосновать простые и наглядные алгоритмы метода последовательных приближений для решения этого уравнения.