Удачным в этом отношении учебником является АиАН 1980 г. (Колмогоров А.Н., Абрамов, Вейц, Шварцбурд, Ивлев Б.М., Иванов-Мусатов).
2. Некоторые рекомендации к изучению производной.
Изучая правила дифференцирования, учащиеся знакомятся с двумя правилами и их выводом:
![]() (1)
(1)
![]() (2)
(2)
![]() и
и 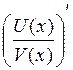 . Правило дифференцирования сложной функции
за исключением случая, когда аргументом сложной функции является линейная
функция, учащиеся не изучают. В выпускных же экзаменационных работах задания с
использованием этих правил встречаются. Поэтому учителю необходимо дать
учащимся эти правила без вывода и отработать их на конкретных примерах.
. Правило дифференцирования сложной функции
за исключением случая, когда аргументом сложной функции является линейная
функция, учащиеся не изучают. В выпускных же экзаменационных работах задания с
использованием этих правил встречаются. Поэтому учителю необходимо дать
учащимся эти правила без вывода и отработать их на конкретных примерах.
Геометрическое истолкование производной функции в точке связано с понятием касательной к графику, прежде всего в этой точке. Чтобы выяснить эту связь, прежде всего необходимо дать определение касательной к графику функции в точке.
Слово «касательная» может ассоциироваться у учеников с
прямой, имеющей одну общую точку с кривой, т.к. они проводили касательную к окружности.
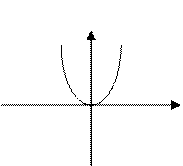
Однако для функции ![]() ученики не назовут касательной
ось oy (одна общая точка) и не сомневаются, что ею будет
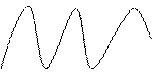
ось ox. Не колеблясь, ученики строят касательные к синусоиде
в точке с абсциссами
ученики не назовут касательной
ось oy (одна общая точка) и не сомневаются, что ею будет
ось ox. Не колеблясь, ученики строят касательные к синусоиде
в точке с абсциссами 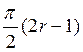 . Не вызывает удивление и случай,
когда кривая в окрестности точки касания располагается по одну сторону от
касательной. И лишь случай, когда кривая в окрестности точки касания лежит по
обе стороны от касательной, вызывает на первых порах недоумение.
. Не вызывает удивление и случай,
когда кривая в окрестности точки касания располагается по одну сторону от
касательной. И лишь случай, когда кривая в окрестности точки касания лежит по
обе стороны от касательной, вызывает на первых порах недоумение.
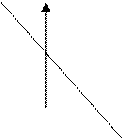
Поэтому в число примеров, предшествующих формулировке определения касательной, необходимо включить такие, чтобы можно было отсеять несущественные признаки и выявить сущность касательной к графику функции.
![]()

![]()
![]()
![]()
![]()
![]()
 а)
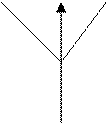
а) ![]() б)
б)
![]() в)
в) ![]()
 |
 |
||
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
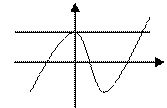
Существенным признаком касательной является «тесное примыкание» ее к кривой в окрестности точки касания.
Ведь именно, представление о функции как о линейной в достаточно малой окрестности точки – основная идея дифференциального исчисления.
Упражнения по теме производная вызывают затруднения у учащихся, особенно:
- нахождение производной функции по ее определению;
- составление уравнения касательной к кривой в точке x0 (№429);
- найти: под каким углом пересекаются графики функции (№423);
- текстовые задачи на max и min (с геометрическим содержанием) №451-461
К таким упражнениям желательно составить алгоритм решения и с помощью алгоритма отработать навыки их решения.
Примеры алгоритмов к упражнениям этой главы смотри «Повышение эффективности обучения математики в школе». Составитель Г.Д.Глейзер, М: Просвещение, 1989 г.
№459
Из
всех прямоугольных треугольников, у которых сумма одного катета и гипотенузы
равна ![]() , найти треугольник с наибольшей площадью.
, найти треугольник с наибольшей площадью.
|
План решения |
Применение плана |
|
1. Строим чертеж. 2. Записываем исходную формулу для вычисления величины, экстремальное значение которой требуется найти. 3. Вводим переменную величину x и выражаем через нее значения всех величин исходной формулы. 4. Подставляя найденные значения величин в формулу, представляем ее как функцию аргумента x. 5. Задаем (по смыслу задачи) область определения функции 6. Функцию аргумента x исследуем на экстремум на найденном числовом промежутке. 7. Записываем ответ. |
Пусть
max
|
Один из вариантов вывод ![]()
Лемма: Если функция
f дифференцируема в точке x0, то ![]() .
.
Доказательство: 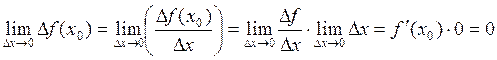 .
.
Следствие: функция, дифференцируемая в точке x0, непрерывна в этой точке.
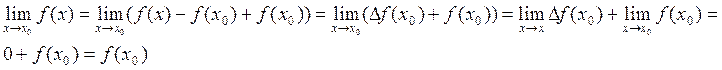
Теорема:
если U и V – дифференцируемы в точке x0, то их произведение дифференцируемо в этой же точке и
![]() .
.
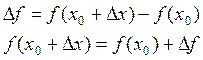
_______________________
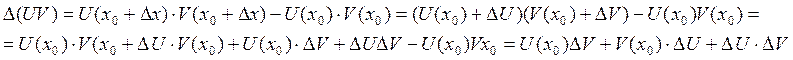
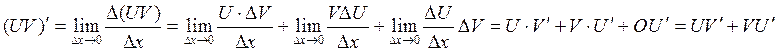
Теорема: если U и V
дифференцируемы в точке x0, функция
![]() , то
, то
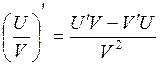
1) 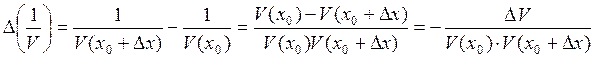
2) 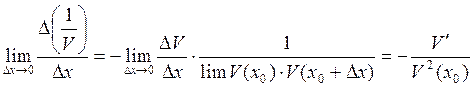
3) 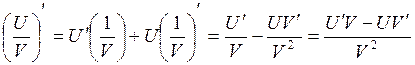
4.082. Найти наименьшее из
значений параметра a, для которых прямая ![]() касается
параболы
касается
параболы ![]() .
.
4.088. Указать большее из
значений параметра b, для которых прямая ![]() касается
параболы
касается
параболы ![]() .
.
4.090 Найти наименьшее
значение функции 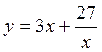 на множестве решений системы неравенств
на множестве решений системы неравенств
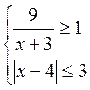
4.091 При каком значении
параметра a прямая ![]() касается графика функции
касается графика функции
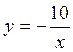
П. Если прямая ![]() является
касательной к параболе
является
касательной к параболе ![]() в точке с абсциссой О,
то
в точке с абсциссой О,
то ![]() равно (-1;1;5;-5).
равно (-1;1;5;-5).
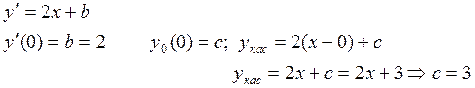
П.В какой точке касательная к графику функции ![]() параллельна прямой
параллельна прямой ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.