Методика изучения производной.
С реформой школы, введением программы А.Н.Колмогорова в старших классах дисциплина «Алгебра и элементарные функции» стала называться «Алгебра и начала анализа». Одним из важнейших понятий математического анализа является понятие, производной, изучаемой в начале учебного года в 11 классе. Важность и полезность понятия производной объясняется возможностью применения этого понятия к широкому кругу задач.
Основная цель изучения данной темы – знакомство с новым математическим аппаратом и не более, в связи с чем в последнем издании АиНА эта тема очень сжата, большинство фактов, формул дается без вывода. Преследуется единственная цель: пополнить арсенал математического аппарата и продемонстрировать его применение в основном при исследовании свойств функций и построение их графиков.
В
последнем издании учебника АиНА определение отличается от традиционного через
предел отношения приращения функции к приращению аргумента. Ныне: lim
разностного отношения, эта формулировка значительно проигрывает. Последнее
издание учебника отличается от предыдущих, изменение в изложении темы сделана в
лучшую сторону. Все формулы производных элементарных функций выводятся очень
доступно, введено понятие критических точек, стационарных точек.
Введено понятие предела функции в точке непрерывности функции, но нет вывода 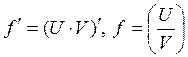 .
.
1. Задачи, приводящие к понятию производной.
Введению понятия производной функции предшествует рассмотрение ряда задач, которые показывают важность предела некоторого вида и тем самым подчеркивают необходимость его изучения. Эти задачи должны быть такими, чтобы при их решении накопилось достаточно материала для обобщений. Они должны быть разнообразными по сюжету; хорошо, если в роли аргумента будут выступать различные переменные, а не только время, как это часто бывает в учебной литературе.
Число задач, которые решаются до введения понятия
производной, не должно быть очень велико, т.к. их решение основано на
вычислении 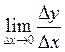 громоздко и однообразно. Достаточно 2-3
задач, различных по сюжету.
громоздко и однообразно. Достаточно 2-3
задач, различных по сюжету.
Задача о теплоемкости тела.
Если температура тела с массой в 1 кг. повышается от ![]() до
до ![]() , то это
происходит за счет того, что телу сообщается определенное количество тепла Q,
значит Q есть функция температуры T, до которой
тело нагревается: Q=Q(T).
, то это
происходит за счет того, что телу сообщается определенное количество тепла Q,
значит Q есть функция температуры T, до которой
тело нагревается: Q=Q(T).
Пусть температура тела повысилась с T до T+![]() T. Количество тепла
T. Количество тепла ![]() Q, затраченное для этого
нагревания, равно
Q, затраченное для этого
нагревания, равно ![]() Q=Q(T+
Q=Q(T+![]() T)-Q(T).
Отношение
T)-Q(T).
Отношение ![]() есть количество тепла, которое необходимо
«в среднем» для нагревания тела на 10 при изменении
есть количество тепла, которое необходимо
«в среднем» для нагревания тела на 10 при изменении ![]() до
до ![]() . Это
отношение называется средней теплоемкостью данного тела в температурном интервале
[T, T+
. Это
отношение называется средней теплоемкостью данного тела в температурном интервале
[T, T+![]() T] и
обозначается Сср.
T] и
обозначается Сср.
Так как средняя температура не дает представления о теплоемкости для любого значения температуры T, то вводится понятие теплоемкости при данной температуре T (в данной точке T).
Теплоемкостью при температуре T (в данной
точке T) называется предел отношения приращения количества
тепла ![]() Q к приращению температуры
Q к приращению температуры ![]() T при условии, что
T при условии, что ![]() T
T![]() 0. Он
обозначается Смгн =
0. Он
обозначается Смгн =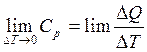 .
.
Задача №2. О скорости химической реакции. Пусть некоторое вещество вступает в химическую реакцию. Количество вещества, вступившее за время t, есть функция от t, т.е. m(t). Определить скорость вступления вещества в момент t0.
[t0, t0+![]() t] Vср=
t] Vср=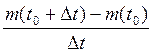
Vмгн=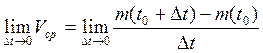
Подводя итог, следует обратить внимание учащихся, что в рассмотренных примерах речь шла о понятии теплоемкости ела при данной температуре как скорости изменения количества тепла при изменении температуры. О скорости химической реакции в момент времени как скорости изменения количества вещества, участвующего в этой реакции, с течением времени.
Отмечается, что введение всех рассмотренных выше
понятий проводилось с помощью предела особого вида, а именно предела отношения
приращения функции к приращению аргумента при условии, что ![]() x
x![]() 0.
После этих задач можно предложить учащимся задачу о нахождении мгновенной
скорости изменения функции.
0.
После этих задач можно предложить учащимся задачу о нахождении мгновенной
скорости изменения функции.
Задача №3. Дать определение скорости изменения функции в точке x0, т.е. мгновенной скорости.
По аналогии с задачами №1,2 назовем на [x0;x0+![]() x] средней скоростью изменения
функции отношение
x] средней скоростью изменения
функции отношение ![]() , мгновенной скоростью функции в
точке x0 назовем
, мгновенной скоростью функции в
точке x0 назовем 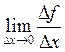 .
.
Таким образом, производная функции в точке есть ее мгновенная скорость.
В связи с изменением целевой установки, связанной с изучением сокращено, и учащиеся не проводят различия между двумя понятиями: производная функции и производная функции в точке, со вторым понятием учащиеся встречаются только в упражнении 783.
Желательно при ознакомлении учащихся с понятием производной заострить их внимание на том факте, что производная функции в точке есть число (и выполнить 2-3 упражнения), а производная функции есть функция.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.