Рассчитать коэффициент парной
корелляции между учитываемыми факторами ![]() и
и
![]()
 . (8)
. (8)
Величина коэффициента корелляции может
изменяться в пределах [-1,+1]. При ![]() - связь между
переменными носит функциональный характер. При
- связь между
переменными носит функциональный характер. При ![]() -
линейная связь отсутствует. Кроме того следует установить достоверность
коэффициента парной корелляции
-
линейная связь отсутствует. Кроме того следует установить достоверность
коэффициента парной корелляции
 ,
(9)
,
(9)
где ![]() .
(10)
.
(10)
Поскольку связь между факторами исследуется по данным
выборки, то необходимо дать оценку значимости выявленной связи. Это
осуществляется путем проверки отличия от нуля найденного коэффициента
корреляции с помощью указанного критерия. Если объем выборки достаточно велик (больше
30-40), распределение коэффициента корреляции можно считать нормальным и, если
выдерживается неравенство ![]() , где 2,6 -
коэффициент t , взятый по таблице нормального
распределения при 0,99 уровня значимости, тогда можно считать, что найденный
коэффициент корреляции значительно отличается от нуля и линейная связь, которую
он характеризует, не случайна. При
, где 2,6 -
коэффициент t , взятый по таблице нормального
распределения при 0,99 уровня значимости, тогда можно считать, что найденный
коэффициент корреляции значительно отличается от нуля и линейная связь, которую
он характеризует, не случайна. При ![]() - наличие линейной
корреляционной связи между параметрами не доказано. Однако и в этом случае
полученный приближенный результат может быть интересен с точки зрения
прогнозирования тенденций развития факторов. Объем расчетов по формулам (4) – (10)
достаточно велик, в связи о этим для выполнения вышеприведенных расчетов
необходимо использование ЭВМ.
- наличие линейной
корреляционной связи между параметрами не доказано. Однако и в этом случае
полученный приближенный результат может быть интересен с точки зрения
прогнозирования тенденций развития факторов. Объем расчетов по формулам (4) – (10)
достаточно велик, в связи о этим для выполнения вышеприведенных расчетов
необходимо использование ЭВМ.
Составить систему нормальных уравнений в
стандартизованном масштабе. Стандартизованный масштаб используется для того,
чтобы сравнить взаимозависимость между различными факторами, имеющими разный
физический смысл и различные единицы измерения. При стандартизованном масштабе
в качестве единицы измерения фактора принимается его среднеквадратическое
отклонение ![]() . Система нормальных уравнений может
быть составлена при использовании формального приема, основанного на идентичности
матриц таблиц коэффициентов парной корреляции и системы нормальных уравнений.
. Система нормальных уравнений может
быть составлена при использовании формального приема, основанного на идентичности
матриц таблиц коэффициентов парной корреляции и системы нормальных уравнений.
Таблица коэффициентов парной корреляции
составляется таким образом, чтобы первым по строкам и столбцам стоял наиболее
значимый независимый фактор X
и далее, по мере уменьшения значимости, помещаются остальные независимые
факторы. Последним фактором должен являться зависимый фектор Т ,
прогнозирование которого интересует исследователя. Столбцы и строки
пронумеровываются. Последняя строка таблицы вычеркивается. Значения
коэффициентов парной корреляции (кроме последнего столбца) умножаются на ![]() , при этом
, при этом ![]() принимается
равным номеру столбца (
принимается
равным номеру столбца (![]() - второй столбец), а
значение коэффициента корреляции фактора, взятого относительно себя, равным
единице. Значения коэффициентов парной корреляции, находящиеся в последнем
столбце, принимаются в качестве свободных членов уравнений соответственно по
строкам. Записывается сумма значений произведений коэффициентов парной
корреляции на
- второй столбец), а
значение коэффициента корреляции фактора, взятого относительно себя, равным
единице. Значения коэффициентов парной корреляции, находящиеся в последнем
столбце, принимаются в качестве свободных членов уравнений соответственно по
строкам. Записывается сумма значений произведений коэффициентов парной
корреляции на ![]() , при этом учитываются
знаки при коэффициентах парной корелляции. Тогда сумма этих произведений по строкам
соответственно даст нормальные уравнения в стандартизованном масштабе
, при этом учитываются
знаки при коэффициентах парной корелляции. Тогда сумма этих произведений по строкам
соответственно даст нормальные уравнения в стандартизованном масштабе
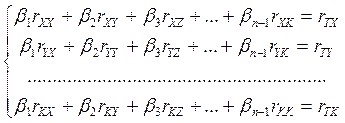 , (11)
, (11)
Решение системы нормальных уравнений дает
коэффициенты ![]() , которые позволяют определить
значение коэффициента множественной корелляции, являющегося характеристикой
тесноты статистической связи между учитываемыми факторами
, которые позволяют определить
значение коэффициента множественной корелляции, являющегося характеристикой
тесноты статистической связи между учитываемыми факторами
![]() .
.
Этот коэффициент изменяется в пределах
[0,1]. При R = 1 - все точки корреляционного пространства лежат на
поверхности регрессии и, следовательно, между факторами существует
функциональная связь. При ![]() - наличие
корреляционной связи не доказано. Чем ближе
- наличие
корреляционной связи не доказано. Чем ближе ![]() к
единице, тем теснее связь между факторами. Квадрат коэффициента множественной
корреляции (коэффициент детерминации) показывает, какая часть величины
колебания зависимой переменной обусловлено величиной включенных в модель
независимых переменных. По величине коэффициента детерминации
к
единице, тем теснее связь между факторами. Квадрат коэффициента множественной
корреляции (коэффициент детерминации) показывает, какая часть величины
колебания зависимой переменной обусловлено величиной включенных в модель
независимых переменных. По величине коэффициента детерминации
![]()
можно оценить точность корреляционной модели.
Значения коэффициентов уравнения множественной регрессии в натуральном масштабе
 ;
;  ;
;
 ; … ;
; … ; 
Значение свободного члена уравнения множественной регрессии
![]()
где ![]() - среднеарифметические значения
зависимого (
- среднеарифметические значения
зависимого (![]() ) и независимых факторов
уравнения множественной регрессии.
) и независимых факторов
уравнения множественной регрессии.
Подставляя найденные значения ![]() в
уравнение множественной регрессии (3) , потенцируют это уравнение. Для оценки
точности модели необходимо провести конкретные расчеты значения функции в
зависимости от значений аргументов независимых переменных и найти среднеквадратическое
отклонение расчетных значений функций
в
уравнение множественной регрессии (3) , потенцируют это уравнение. Для оценки
точности модели необходимо провести конкретные расчеты значения функции в
зависимости от значений аргументов независимых переменных и найти среднеквадратическое
отклонение расчетных значений функций ![]() от
их опытных данных» принятых в качестве исходных:
от
их опытных данных» принятых в качестве исходных:
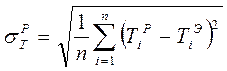 ,
,
где ![]() - значения функции
расчетное и экспериментальное. Затем следует рассчитать коэффициент вариации.
Для этого определяется среднеарифметическое значение расчетных значений функции
- значения функции
расчетное и экспериментальное. Затем следует рассчитать коэффициент вариации.
Для этого определяется среднеарифметическое значение расчетных значений функции
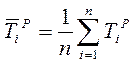 ,
,
и коэффициент вариации
![]() .
.
Если коэффициент вариации
достаточно мал (![]() ) то результаты расчета могут
быть признаны удовлетворительными.
) то результаты расчета могут
быть признаны удовлетворительными.
Таким образом, зная величины
характеристик существующего оборудования (зависимых факторов), можно
прогнозировать величину интересующего (зависимого) фактора. Очевидно, что
систему нормальных уравнений (11) можно построить (при одних и тех же коэффициентах
парной корреляции), сделав зависимым любой из выбранных факторов ![]() . Для этого необходимо лишь
изменить положение коэффициентов парной корреляции в таблице.
. Для этого необходимо лишь
изменить положение коэффициентов парной корреляции в таблице.
1.7. Оптимальный выбор структуры ГПС в условиях неопределенности
развития производства
При управлении ТП часто возникает необходимость принятия решения в условиях неопределенности. Неопределенность при анализе ТП появляется из-за неполного знания общей физической и статистической природы явлений, происходящих в технологических и социальных системах. В этих случаях необходим математический аппарат, позволяющий принять решения в условиях ограниченной информации и выбрать оптимальные варианты. Подобные задачи в математике анализируются в теории игр и статистических решений [1,2,5] .
Во многих случаях необходимо определить оптимальное поведение по отношению к противодействующей стороне (противника), действие которой случайно. В этом случае возникает конфликтная ситуация, определяющаяся как игра, для которой формируют математическую модель и определяют правила игры, т.е. определяются противодействующие стороны (игроки) и исход конфликта (выигрыш или проигрыш).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.