При моделировании были получены следующие параметры:
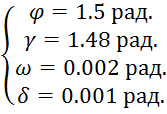,при t
=10 сек. 
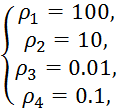и
k=0.001
Результаты моделирования представлены в приложении Б.
В данном случае ЛА выходит на заданные углы по
окончанию маневра, а варьированием параметров 
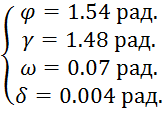,при t
=10 сек. 
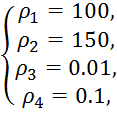и
k=0.001
можно добиться получения семейства оптимальных траекторий
В случае, если ограничения на управление не
используются , то ЛА теряет устойчивость при определенной комбинации параметров
Результаты представлены в приложении В
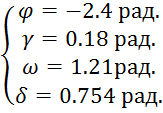,при t
=10 сек. 
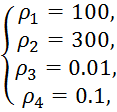и
k=0.001
Однако , есть ограничения на управления учесть , то при тех же параметрах получим:
Результаты моделирования данного случая представлены в приложении В.
6. Сравнение результатов с известными решениями
Для задач оптимизации динамических систем, в частности, систем управления, применяют особую форму записи уравнений для определения допустимых экстремалей – с использованием функции Гамильтона. Эта форма получила наиболее широкое распространение для задач с дифференциальными связями и принята за основу в методах оптимизации систем при наличии ограничений в форме неравенств.
Рассмотрим задачу синтеза оптимального управления для объекта, модель которого задана в виде (23.1). Такая задача может рассматриваться как задача Лагранжа, причем модель объекта дает n дифференциальных связей (аргумент t в явном виде далее не учитывается для сокращения записи):
, i=1,2,...,n, (27)
а критерий качества приводится к функционалу:
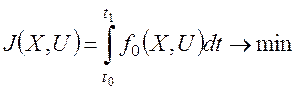. (28)
При решении такой задачи составляют функцию Лагранжа
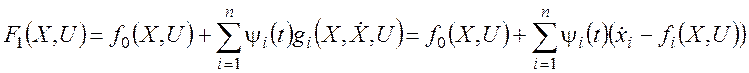, для которой
далее записывают систему уравнений Эйлера-Лагранжа и применяют другие условия
достижения экстремума.
Если дифференциальные связи приводятся к форме (21) или (27), может быть введена функция Гамильтона
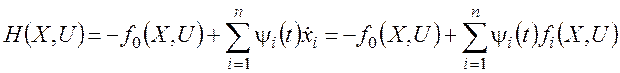. (29)
Сравнивая выражения, нетрудно установить взаимно однозначное соответствие между функциями Лагранжа и Гамильтона:
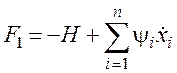или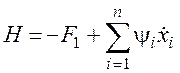 
. (30)
Функции yi(t) называются сопряженными переменными. Они могут быть определены по функции Гамильтона (29
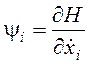, i=1,2,...,n. (31)
Запишем уравнения Эйлера-Лагранжа, учитывая (30):
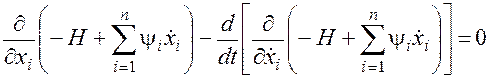, i=1,2,...,n;
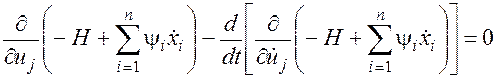, j=1,2,...,r.
Раскрыв скобки и продифференцировав, получим:
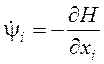, i=1,2,...,n; (32)
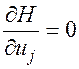, j=1,2,...,r. (33)
Полученная система уравнений (25.5)-(25.7) называется системой уравнений Эйлера-Лагранжа в канонической форме.
Рассмотрим условия трансверсальности.
Для подвижных концов на основе (24.5) с учетом (25.3) получим:
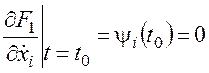или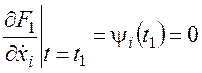 
. (34)
Для свободных концов на основе (24.6) с учетом (25.3), (25.8):
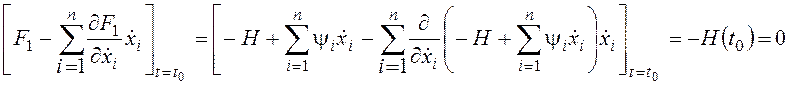
или 
.
(35)
При работе с функцией Гамильтона вместо (34), (35) обычно применяется следующее общее выражение для условий трансверсальности:
.
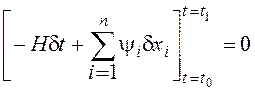(36)
Запись в форме (25.10) трактуется следующим образом:
- заключенное в скобки условие применяется как для левой t=t0, так и для правой t=t0 границ (концов временного интервала);
- если рассматриваемая граница задана, для нее вариация dt=0, если задано граничное условие xi0 или xi1, для данной границы и соответствующего iвариация dxi=0, следовательно все слагаемые в (36), содержащие такие вариации, тождественно равны нулю;
- для всех отсутствующих в задаче граничных условий соответствующие вариации dt и dxi являются ненулевыми и взаимно независимыми, следовательно, условие (36) будет выполняться только при равенстве нулю соответствующих сомножителей при вариациях, то есть при выполнении системы условий (34)-(35).
Рассмотренная система необходимых и достаточных условий достижения экстремума функционала в рамках вариационного исчисления обеспечивает получение локальных экстремумов. Этого вполне достаточно в задачах без ограничений на переменные состояния объекта управления или на управляющие сигналы. Если область допустимых управлений не ограничена, абсолютный экстремум совпадает с локальным. Если в задаче рассматривается некоторая ограниченная область допустимых состояний или управлений, задачу оптимизации нельзя свести к определению локального экстремума. Абсолютный экстремум в ряде случаев может совпадать с границей допустимой области.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.