Бесстолкновительные явления при наличии пространственного заряда, страница 14

                П = (I /V^3/2)/(χb/a)                                                                                      (2.116)

 

С его помощью уравнение (2.92)  можно переписать в виде

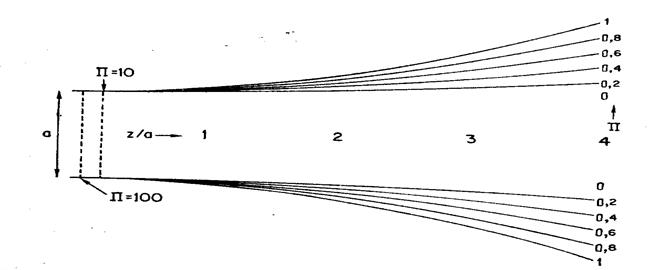
(x/a) = ( 1/2) + ( 1/18) П(z/а)²;                                                       (2.117)

график х(z) показан на рис. 2.16 для разных значений П. Как можно заметить, если расширение заряженного пучка мало, то нормированный первеанс должен быть малым по сравнению с единицей.

Если пучок вначале однороден, то поперечная сила, действующая на ион, пропорциональна, как следует из (2.104), расстоянию от медианной плоскости. Это приводит к расширению пучка при сохранении его однородности в поперечном направлении. Полезно отметить еще раз, что выводы, сделанные в данном разделе, базируются на предположениях, что в ионном пучке отсутствует разброс по скоростям и направлениям и он не содержит других заряженных частиц, таких, как электроны или медленные ионы. Ситуации, более адекватные реальным условиям, будут рассмотрены ниже.

Б. Аксиально-симметричные пучки, нормированный первеанс <1

Рассмотрим теперь пучок круглого сечения. Как и раньше, считаем, что все ионы имеют одну и ту же скорость и движутся вначале параллельно оси, а также, что влияние пространственного заряда достаточно мало, так что изменением потенциала в пучке можно пренебречь. Если рассматривать очень малые углы расходимости, то можно считать поле чисто радиальным и использовать закон Гаусса; тогда имеем

Е_r = (Jr/2ε₀) (2eV/M)^-1/2.(2. 1 18)

Чтобы определить, насколько большим может быть ток для того, чтобы выполнялось предположение о малости пространственного заряда, проинтегрируем Е_r от нуля до радиуса пучка r₀ и получим

ΔV = (Jr²₀/4ε₀) (2eV/M)^-1/2,                                                             (2.119)

что приводит к соотношению          

(ΔV/V) = (I/4πε₀) (2e/M)^-1/2V ^-3/2,                                                               (2. 120)

где мы положили I=πr²₀J. Можно написать

ΔV/V=П/9π,                                                                          (2.121)

где П — нормированный первеанс, определенный из (2.116) при b= а, т. е.

                                                    П= I /χ  V^3/2                                                                                      (2.122)

Как и в случае длинных узких пучков, можно считать, что изменения потенциала в пучке малы при П ≤ 1

Следует также рассмотреть расстояние до окружающей пучок стенки, предположительно цилиндрической. Вне пучка поле уменьшается по закону 1/r и интегрирование дает выражение

                                                                   (2.123)

где ΔV ' — падение потенциала между поверхностью пучка и окружающей стенкой радиуса R. Ситуация здесь гораздо более благоприятна, чем в случае длинных узких пучков, и до тех пор пока отношение R / r₀ не станет большим, можно считать ΔV '/V << 1 для значений П ≤ 1.

Из  (2.118)     можно    найти    радиальное    ускорение    иона (e/M)E_r на кромке пучка. Получим

d²r/dt² = (I/2πε₀r) (e/2MV)^1/2.(2. 124)

Интегрируя один раз, имеем

(dr/dt)²=(I/πε₀) (e/2MV)^1/2In (r/r₀) ,                                                                   (2.125)

причем константа интегрирования выбрана из условия dr/dt = 0 при r=r₀. Заменяя t координатой z=, получим уравнение

dr/dz=(I/2πε₀)^1/2(M/2e)^1/4V^-3/4In^1/2 (r/r₀),                                        (2.126)

что приводит к соотношению

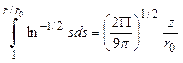                                                                                      (2.127)

Если положить In^1/2 s = u, то получим

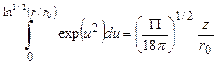                                                            (2.128)

Хотя мы ввели нормированный первеанс, это уравнение эквивалентно уравнению Фаулера — Гибсона [102]. Интеграл в (2.128) можно свести к интегралу Доусона

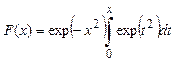,                                                                  (2.129)