Анализ движения заряженных частиц в разрядах с осциллирующими электронами, страница 6

l ~ 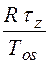 ~  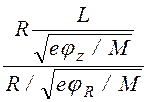                                           (1.2.4)

составляет величину больше или порядка l, то вероятностью столкновений уже нельзя пренебречь даже при формальном выполнении условий кнудсеновского режима l>>L,R. Для глубины потенциальной ямы в этом случае получаем

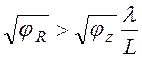                                                                (1.2.5)                                     либо в случае j_z << kT/e.

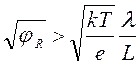                                                                (1.2.6)

При движении против продольного электрического поля ( v_z <0, если  E_z = -dj₀ / dz > 0) частица будет иметь скорость v_z  при прохождении точки z, если она имела после  ионизации  или  последнего столкновения в точке z' > z скорость         

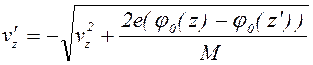= - v¢(z¢)                    (1.2.7) и прошла путь от z' до z без столкновений. При движении по полю (v_z>0) скорость v_z   в точке  z  могут иметь как частицы, получившие в момент образования в точке  z'  положительную компоненту v_z' = v'(z'), так и частицы, имевшие скорость v_z' = - v'(z'), но зaтормoзившиеся в электрическом поле и набравшие скорость  v_z  при обратном движении от точки поворота  дo z. Для  получаем соотношение

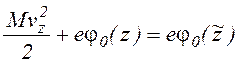.                                              (1.2.8)

Если (1.2.8) не имеет решений в промежутке [0,L], то очевидно, частица, имевшая в  z'  скорость v_z' = - v'(z'), пересекает границу z=0 и выбывает из рассмотрения. Поэтому обладать в точке z скоростью v_z > 0, удовлетворяющей условию                

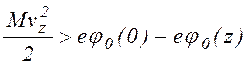,                                              (1.2.9)

будут лишь частицы, имевшие в точке  z'  положительную компоненту  v_z'. Принимая распределение по скоростям образующихся  после ионизации или последнего столкновения  частиц  максвелловским, запишем распределение образующихся в единицу времени в точке z  частиц по амплитудам и продольным скоростям в виде

S₀[z,v_z,a] = f_m(v_z)(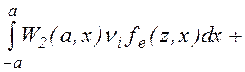  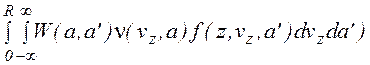        +,                     (1.2.10)

где n(v_z,a) - усредненная по периоду колебаний частота столкновений частицы, имеющей скорость v_z и амплитуду a. Таким образом, интегральное уравнение для  f(z,v_z,a)  принимает следующий вид (1.2.11)

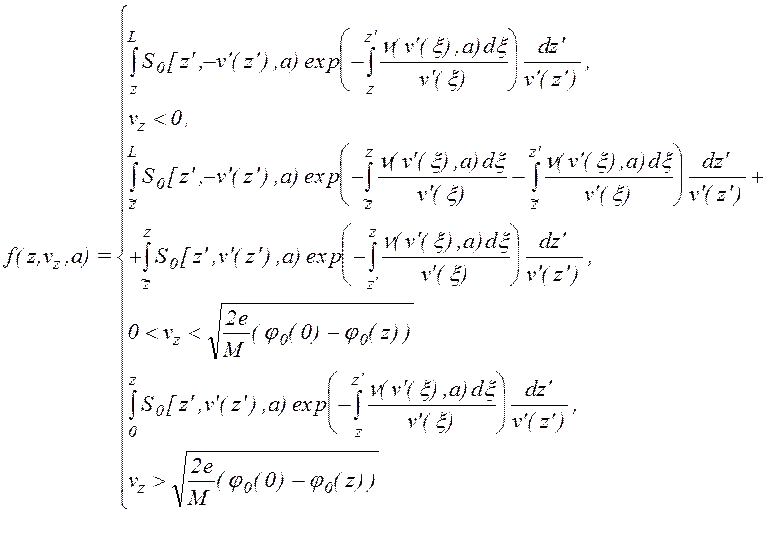          Pассмотрим возможные упрощения интегрального  уравнения  в различных предельных случаях. Если частота ухода частиц как в продольном, так и поперечном направлении много  меньше  характерной частоты столкновений (что выполняется при  L>>l, j_R>>kT/e), то можно принять, как это предложено в [86], поперечное  распределение Больцмановским 

f_os(x,z)=f₀(z)exp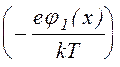.                                     (1.2.12)

Усредняя поперечное распределение, введем функцию

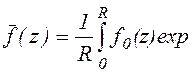
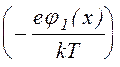dx.                              (1.2.13)

При выполнении условия  eEl << kT  функцию  можно найти используя диффузионное приближение                        

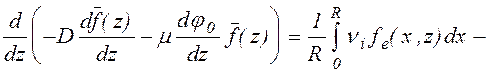
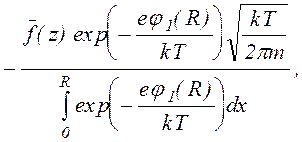                                      (1.2.14)

Первый  член  в правой части  (1.2.14)  представляет собой усредненную по  x  частоту образования частиц в результате ионизации, а второй  учитывает возможный уход частиц в поперечном направлении  способом, предложенным в  [86], поскольку

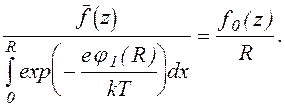                                  (1.2.15)

Если eE_zl>>kT, то можно пренебречь тепловым разбросом  продольных скоростей ( S₀[z,v_z,a] = S₀[z,a]f_m(v_z)® S₀[z,a]d(v_z) )  и  (1.2.11)  принимает вид

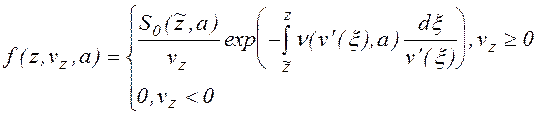  (1.2.16) где   - корень уравнения  (1.2.8) .

Аналогичное упрощение можно провести для поперечного  распределения, но следует заметить, что замена  f_m(v_x)® d(v_x)  может привести к существенным ошибкам в расчете  f(a)  при  малых a, так как для частицы,  образовавшейся вблизи оси , потенциальная энергия мала и может быть меньше или порядка тепловой, в частности, если f(a=0)0,  то  f_os(x=0)=¥, поскольку dj/da_a=0 = 0 (см.1.1.14). Учет теплового движения также необходим вблизи  края  потенциальной ямы.

Если L<<l и , то столкновениями можно пренебречь, и тогда (1.2.16) преобразуется к виду

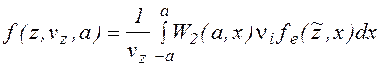                           (1.2.17)