Анализ движения заряженных частиц в разрядах с осциллирующими электронами, страница 4

          G(a)= 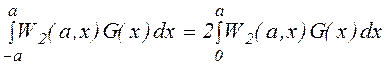,           (1.1.17)

где G(x)=n_in_f(x), n_i - частота ионизации, отнормированная на 1 быстрый электрон, а n_f  - концентрация быстрых электронов, W₂(a,x) - плотность вероятности для частицы, образовавшейся  в точке х приобрести амплитуду колебаний a.

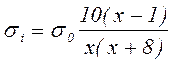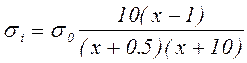В [87] показано, что для большинства газов сечение ионизации аппроксимируется зависимостями вида  или  где 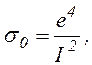 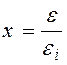, e_i - пороговая энергия ионизации. В характерном для быстрых частиц в рассматриваемых разрядах диапазоне энергий 100 - 1000 эв ионизационное сечение с вполне приемлемой для оценочных расчетов точностью можно аппроксимировать зависимостью вида  или , что позволяет считать ионизационную частоту константой. При проведении более точных расчетов для вычисления частоты необходимо провести усреднение по спектру быстрых электронов.

Для W₂ выполняется следующее соотношение

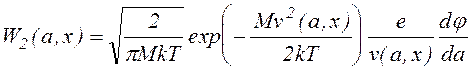,      (1.1.18)

Изменение энергии частиц в случае слабоионизованного газа происходит в основном в результате их столкновений  с атомами, для учета которых широко применяется модельный интеграл [88], учитывающий сохранение числа частиц

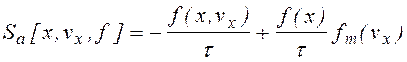,                    (1.1.19)

где t - характерное время между столкновениями,  f_m  - максвелловская функция. Как видно из  (1.1.19), для любой частицы частота столкновений считается одинаковой  n(a)=1/t , и в результате столкновений образуются частицы с максвелловским распределением по скоростям, следовательно

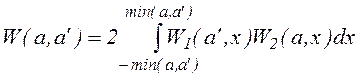,                          (1.1.20)

где  2W₁(a',x)dx  - вероятность для частицы с амплитудой  a'  испытать столкновение в слое  dx, при условии, что  столкновение произошло.

Следует заметить, что при значительных отклонениях  функции распределения от равновесной использование  модельного  интеграла  (1.1.19) для расчета ионного распределения является  нецелесообразным, поскольку основным для ионов в собственном  газе  является процесс перезарядки, сечение которой s_tr слабо зависит от скорости и для частиц, обладающих высокими  скоростями,  частота столкновений увеличивается. При учете перезарядки обычно принимают s_tr ~ const . При таком допущении

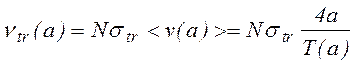,                            (1.1.21) а вероятность  перезарядки в любой точке x внутри промежутка [-a,a]  одинакова

W_tr(x,a) = .                                                                   (1.1.22)

В процессе перезарядки взаимодействующие  частицы  практически не меняют своих скоростей, поэтому распределение вновь образованных ионов по скоростям можно принять максвелловским с температурой равной температуре нейтрального газа,  следовательно

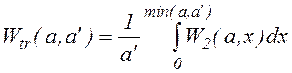.                                       (1.1.23)

Если решение уравнения  (1.1.16)  найдено, то перейдя  от   f(a) к f_os(x,v_x) можно затем определить явный вид интеграла столкновений и проинтегрировать уравнение  (1.1.8)  для  f_es(x,v_x). В момент времени  t  в точке  x  скорость  v_x будут  иметь  частицы, образовавшиеся в некоторый момент времени  t'<t, в точке  x'  со скоростью v_x', где x,v_x,t   и x',v_x',t'  связаны следующими соотношениями

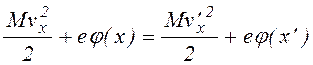,                                    (1.1.24)

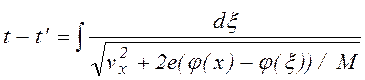.                            (1.1.25)

Интегрируя по всем возможным  t', получим

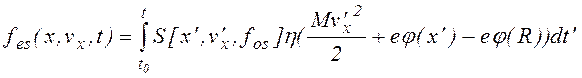.   (1.1.26)

Переходя от интегрирования по времени к интегрированию по координате  dt'=dx'/  и используя модельный интеграл столкновений  (1.1.19) , получим в стационарном случае

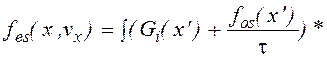
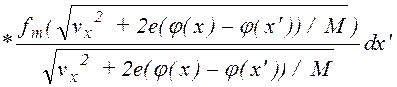                       (1.1.27)

Интеграл берется в пределах от -R до  x, при v_x >  и от x до R, при v_x < - , f_es(x,v_x)=0 при остальных  v_x.

Если потенциал j(x) заранее неизвестен,  a  подлежит определению, то необходимо совместное решение уравнений  (1.1.15), (1.1.16) и  (1.1.27)  с уравнением Пуассона или квазинейтральности .  В этом случае удобнее преобразовать  (1.1.15), (1.1.16)  так, чтобы получить связь между  f_os(x)  и j(x). Используя  (1.1.15) , выразим  f(a)  через f_os(x). При  x>0  перепишем  (1.1.15)  в виде

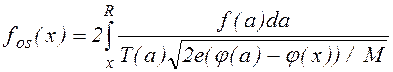.                      (1.1.28)

Домнoжая обе части  (1.1.28)  на   и интегрируя по  dx  в пределах от  y  до  R, получим