Методическое пособие для подготовки к лабораторным работам по темам: Волновая оптика. Квантовая оптика. Квантовая механика и ядерная физика, страница 30

Общая погрешность прямого измерения состоит из случайной и приборной погрешностей. Поскольку доверительные вероятности этих ошибок могут различаться, при расчете результирующей (суммарной) погрешности Dx следует учесть данное различие. Как следует из вышеизложенного, приборная погрешность имеет высокую доверительную вероятность, приближающуюся к единице. Истинный же закон распределения приборных ошибок в партии приборов данного типа неизвестен. Один из возможных способов оценки суммарной погрешности в этом случае заключается в следующем. Полагают, что закон распределения приборных погрешностей близок к нормальному. Тогда величина Dx_пр примерно соответствует "трёхсигмовому" интервалу. Доверительный интервал для используемой нами надёжности результата 0,95 равен "двухсигмовому", т.е. он составляет величину 2·Dx_пр / 3. Воспользовавшись правилом «накопления ошибок» (4.3), найдём общую погрешность прямого измерения в виде

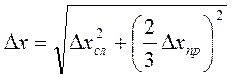                                                               (4.4)

Следует иметь в виду, что складывать приборную и случайную погрешности по формуле (4.4) имеет смысл лишь в том случае, если они различаются меньше чем в три раза. Если же одна из погрешностей больше другой в три и более раз, именно её и следует принять в качестве меры общей погрешности. Экспериментатор должен стремиться к тому, чтобы случайная погрешность была меньше приборной и не вносила вклад в общую погрешность. Однако на практике не всегда удаётся провести достаточно большое число измерений и приходится пользоваться правилом сложения (4.4).

РАСЧЕТ ПОГРЕШНОСТЕЙ ДЛЯ СЛУЧАЯ
КОСВЕННЫХ ИЗМЕРЕНИЙ

При проведении научно-технических исследований в большинстве случаев искомую физическую величину не удаётся измерить непосредственно, а приходится рассчитывать по формулам, в которые в качестве одной или нескольких переменных входят величины, измеряемые с помощью приборов. Такие измерения, как уже отмечалось, называются косвенными. Рассмотрим методику расчёта погрешностей для случая косвенных измерений.

Допустим, необходимо определить некоторую физическую величину f, которая связана функциональной зависимостью с величинами u, v, w,… .

f = f(u, v, w,…)                                                       (5.1)

Величины u, v, w,… измеряются непосредственно с помощью приборов. Пусть было проведено по п измерений каждой из величин u, v, w,… и получены следующие результаты:

                    u₁, u₂,…,u_n

                    v₁, v₂,…,v_n                                                                                              (5.2)

                    w₁, w₂,…, w_n                                                          

Результаты прямых измерений (5.2) были обработаны согласно правилам, изложенным в разделе 3 и 4, и определены средние значения и соответствующие им погрешности:

;;.             (5.3)

Наилучшей оценкой истинного значения искомой величины f является её среднее значение . Для нахождения необходимо в формулу (5.1) подставить средние значения прямо измеренных величин:

              = f()                                                     (5.4)

Очевидно, что величина получена с некоторой погрешностью . Погрешность при косвенном измерении зависит от погрешностей прямо измеренных величин и вида функциональной зависимости (5.1).

Если прямые измерения проведены независимыми способами и относительные погрешности ε(u), ε(v), ε(w),... невелики, то теория погрешностей даёт следующую формулу для нахождения погрешности:

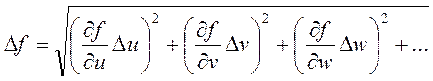  ,                         (5.5)

где , , ,.... - частные производные от функции (5.1), которые вычисляются при , , ,... .

Пусть зависимость (5.1) имеет степенной вид

               ,                                                           (5.6)

где А - некоторая константа; α, β, γ показатели степени (целые или дробные, положительные или отрицательные). В этом случае для расчета ∆f удобнее использовать формулу

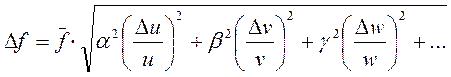                (5.7)

Поясним, как получается формула (5.7). Для этого предварительно прологарифмируем уравнение (5.6)

ln f = ln A + α ln u + β ln v + γ ln w                                   (5.8)

Известно, что 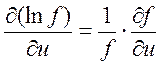, отсюда получаем                

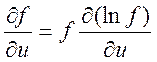                                                                                   (5.9)

Вычислив частную производную и подставив её в (5.9), получим

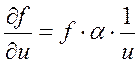                                                                                      (5.10)

Далее, заменяя в (5.5) частные производные выражениями вида (5.10), придем к формуле (5.7).

Рассмотрим два примера. 1. Дана функция .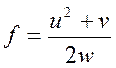

Пусть средние значения и погрешности прямо измеренных величин и, v и w равны, соответственно, , , , ∆u, ∆v и ∆w. Найдем формулу для расчета погрешности ∆f.

Для нахождения ∆f применим правило (5.7), предварительно вычислив частные производные функции f:

;  ; 

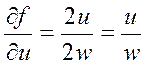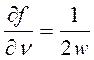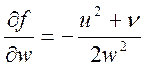
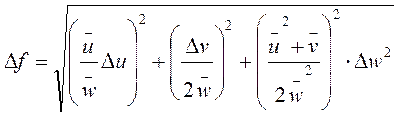
2. Пусть функция f имеет другой вид: 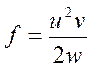. В этом случае, используя правило (5.7), запишем:

;   

6. ПОСЛЕДОВАТЕЛЬНОСТЬ ОПЕРАЦИЙ ПРИ ОБРАБОТКЕ

РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ

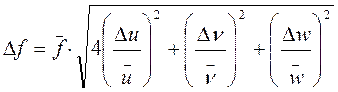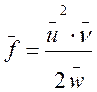
1. Рабочую формулу для искомой величины преобразовать так, чтобы в неё входили непосредственно измеряемые величины – u, v, w,…

                        f = f (u, v, w, …)                                        (6.1)

2. По результатам прямых измерений величин u, v, w,… (см. (5.2))  рассчитать средние значения:

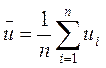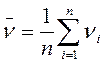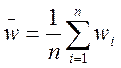;   ;                               (6.2)

3.   Рассчитать среднее значение искомой величины

                    = f (, , , …)                                                         (6.3)

4.   Определить по классу точности или цене наименьшего деления приборные погрешности непосредственно измеряемых величин:

             ∆u_пр, ∆v_пр, ∆w_пр, …                                                          (6.4)

5. Для каждой из величин u, v, w, … определить величину случайной погрешности с доверительной вероятностью 0,95. Например, для величины u рассчитав

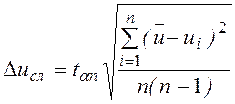                                                  (6.5)