Решение уравнения теплопроводности

ОТЧЕТ

Методы вычислений

Задание 1

Выполнила:

Бах Татьяна, гр. 3113

Проверила:

Аверина Т.А.

Постановка задачи

Необходимо найти решение уравнения теплопроводности, удовлетворяющее некоторым начальным и краевым условиям, т.е. решить следующую начально-краевую задачу:

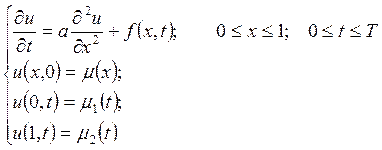
В программе реализовано численное решение этой задачи при следующих данных:

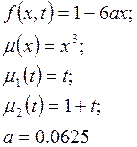
Точное решение задачи при таких правой части, начальных и краевых условиях известно:

Метод

Для численного решения дифференциальной задачи необходимо перейти к разностной задаче. Для нахождения решения сначала попробуем использовать следующую трехслойную разностную схему:

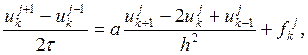                                                 (1)

т.е. полностью сеточная задача будет выглядеть так:

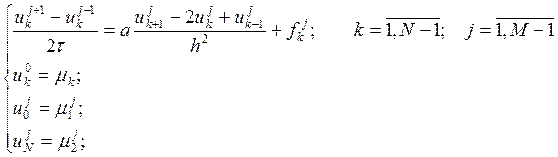
При исследовании разностной схемы (1) увидим, что она абсолютно неустойчива, а значит, неприменима для нахождения решения. Если ее немного преобразовать, то можно получить другую трехслойную схему:

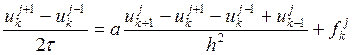                                          (2)

Разностная схема (2) называется схемой Дюфорта-Франкела, и она является абсолютно устойчивой. В итоге схема (2) и будет использоваться для нахождения численного решения задачи.

Свойства метода

Точность схемы (1)

Сначала определим, насколько хорошо эта схема аппроксимирует нашу дифференциальную задачу. Погрешность аппроксимации считается по следующей формуле:

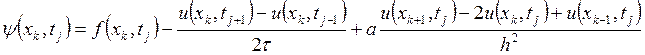
Разложим все стоящие в правой части функции в ряд Тейлора в точке . Для сокращения записи аргументы писать не будем:

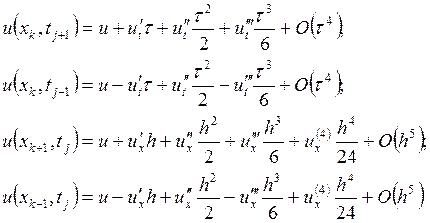
Подставляя эти разложения в формулу для подсчета погрешности аппроксимации, и учитывая то, что , получаем:

.

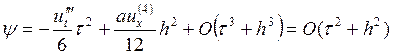Значит, при  схема (1) аппроксимирует нашу дифференциальную задачу. Аппроксимация абсолютная.

Устойчивость схемы (1)

Для исследования устойчивости попробуем искать решение уравнения 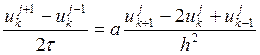 в виде . Подставим такое решение в схему, сразу сократим на . Получаем: 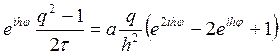. Преобразуем это выражение в квадратное уравнение на :

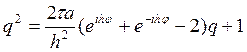
Так как 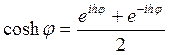, и 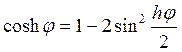то уравнение приводится к такому виду:

.

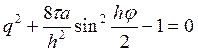Решая это квадратное уравнение, видим, что один из его корней всегда больше 1, т.к. корни имеют следующий вид: 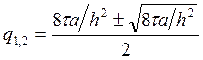. Значит, схема (1) абсолютно неустойчива.

Точность схемы (2)

Заменим схему (1) на (2), и будем теперь решать такую разностную задачу:

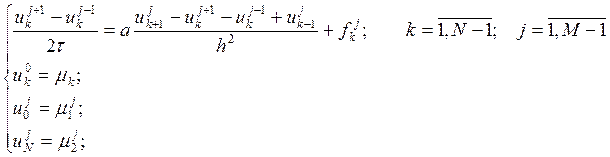
Сначала определим, насколько хорошо эта схема аппроксимирует нашу дифференциальную задачу. Погрешность аппроксимации считается по следующей формуле:

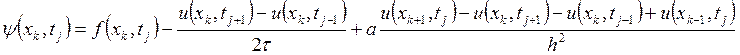
Разложим все стоящие в правой части функции в ряд Тейлора в точке . Для сокращения записи аргументы писать не будем:

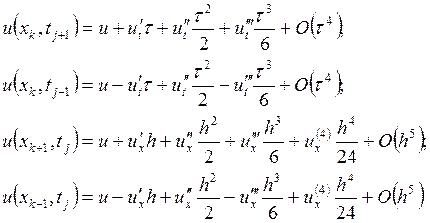
Подставляя эти разложения в формулу для подсчета погрешности аппроксимации, и учитывая то, что , получаем:

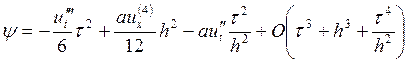                                (3)

Формула (3), в которой явно выписан главный член аппроксимации, нам еще понадобиться. А пока можно записать погрешность аппроксимации в более простой форме:

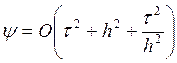
Значит, при  схема (2) аппроксимирует нашу дифференциальную задачу. Но аппроксимация получается условной – необходимое условие: .

Устойчивость схемы (2)

Исследуем разностную схему (2) на устойчивость. Для начала перепишем ее в форме, позволяющей явно вычислять значение сеточной функции на очередном слое:

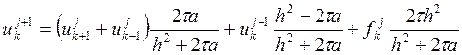
Запишем одно из определений устойчивости: разностная схема устойчива, если существует не зависящие от  константы , такие что для любой правой части  и любых начальных данных  выполняется оценка:

Докажем абсолютную устойчивость разностной схемы (2) с помощью этого определения. Используя то, что , оценим:

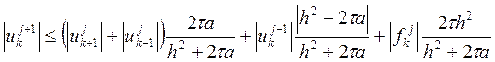
Обозначив 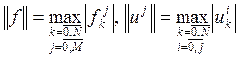, получаем новую оценку решения:

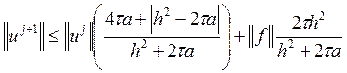
Теперь нужно рассмотреть 2 случая – в зависимости от знака выражения, стоящего под знаком модуля, получатся разные оценки.

Пусть , т.е. .

Тогда 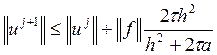. Формула верна для , а . Применяя это соотношение М раз, получаем:

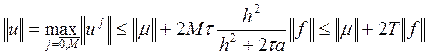, так как , и .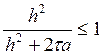

Значит, в этом случае определение устойчивости выполняется, т.к. есть не зависящие от  константы  и .

Второй случай рассматривается аналогично. Для оценки нормы функции на слое выводится рекуррентная формула, которая затем применяется М раз, и получается оценка нормы функции на всей сетке, удовлетворяющая неравенству из определения устойчивости.

В итоге для разностной схемы (2) доказана аппроксимация и устойчивость. Значит, по теореме сходимости, которая утверждает, что при наличии аппроксимации из устойчивости следует сходимость, решение разностной задачи будет сходиться к решению дифференциальной. Т.е. можем применять поставленную сеточную задачу для нахождения численного решения исходного уравнения.

Численные эксперименты

Все эксперименты будет проводить при .

Схема (1)

При любых  и  получившееся решение разностной задачи не имеет ничего общего с решением дифференциальной задачи. Например, были взяты такие значения:

		Номер слоя
0.05	0.05	12
0.01	0.05	28

В этой таблице выписан номер слоя по времени, на котором погрешность решения становится порядка 1, т.е. порядка самого решения.

Этот эксперимент подтверждает теорию. Так как схема (1) не является устойчивой, то решение разностной задачи к решению дифференциальной сходиться и не должно. Поэтому для нахождения численного решения эту схему использовать нельзя.

Схема (2)

Выше было доказано, что решение разностной задачи, построенной по схеме (2), должно сходиться к решению дифференциальной, причем точность должна быть порядка . Значит, взяв, например,  и , мы можем ожидать погрешность решения . В следующей таблице приведены результаты численного эксперимента:

		Погрешность решения
0.04	0.2
0.01	0.1
0.0025	0.05

На первый взгляд, результат получился довольно странный. Во-первых, погрешность решения намного меньше, чем ожидалось. Во-вторых, при уменьшении  в 2 раза погрешность вроде бы должна уменьшится в 4 раза. А она почему-то увеличивается. В чем же дело?

Посмотрим на выражение (3), в котором явно выписан главный член погрешности аппроксимации:

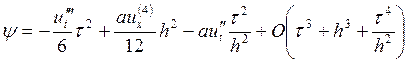                                (3)

В этом выражении функция  - это точное решение дифференциальной задачи. Оно нам известно: . Можем посчитать производные функции , входящие в выражение (3): .

Так как все производные тождественно равны нулю, то погрешность получается просто нулевая (перед большими степенями  и  будут стоять производные более высоких порядков, которые, конечно, тоже нулевые). Значит, при заданных правой части, начальных и краевых условиях численное решение разностной задачи не просто сходится к решению дифференциальной задачи, а в точности совпадает с ним. Ошибки, которые мы видим в таблице – просто ошибки округления при выполнении математических операций на ЭВМ (тип Real содержит 12 знаков в дробной части числа, поэтому погрешность получается ). При уменьшении  в 2 раза  уменьшается в 4 раза, т.е. количество слоев по времени в 4 раза возрастает. Значит, значительно возрастает и количество операций, поэтому увеличивается погрешность.

Результаты всех численных экспериментов, оказывается, не противоречат теории, как может показаться сначала, а в точности подтверждают ее.