Решение уравнения переноса

ОТЧЕТ

Методы вычислений

Задание 2

Выполнила:

Бах Татьяна, гр. 3113

Проверила:

Аверина Т.А.

Постановка задачи

Необходимо найти решение уравнения переноса, удовлетворяющее некоторым начальным и краевым условиям, т.е. решить следующую начально-краевую задачу:

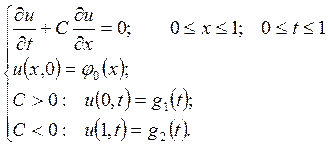
В программе реализовано численное решение этой задачи при следующих данных:

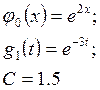
Точное решение задачи при таких начальных и краевых условиях известно:

Метод

Для численного решения дифференциальной задачи необходимо перейти к разностной задаче. Для нахождения решения используется следующая разностная схема:

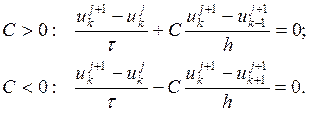
Эта схема называется неявной схемой бегущего счета.

Свойства метода

Точность схемы

Исследуем точность неявной схемы бегущего счета при . Определим, насколько хорошо эта схема аппроксимирует нашу дифференциальную задачу. Погрешность аппроксимации будем считать в точках  по следующей формуле:

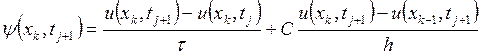
Разложим все стоящие в правой части функции в ряд Тейлора в точке . Для сокращения записи аргументы писать не будем:

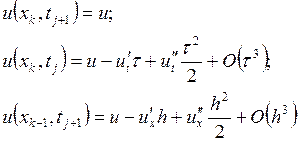
Подставляя эти разложения в формулу для подсчета погрешности аппроксимации, получаем:

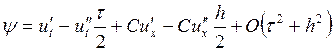                                             (1)

Формула (1) нам еще понадобиться для дальнейшего исследования свойств разностной схемы. А пока можно воспользоваться тем, что  - решение дифференциального уравнения в точке , т.е. что , и записать погрешность аппроксимации в более простой форме:

.

Значит, при  разностная схема аппроксимирует нашу дифференциальную задачу с порядком аппроксимации .

При  погрешность аппроксимации определяется аналогично. По разностной схеме составляется формула, в нее подставляются разложения функций в ряд Тейлора, и в итоге получается:

.

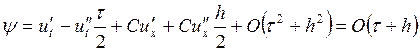Порядок аппроксимации один и тот же, независимо от знака С.

Устойчивость схемы

Исследуем разностную схему на устойчивость при . Для начала перепишем ее в форме, позволяющей явно вычислять значение сеточной функции в очередной точке:

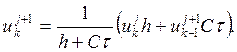
Запишем одно из определений устойчивости: разностная схема устойчива, если существует не зависящие от  константы , такие что для любой правой части  и любых начальных данных  выполняется оценка:

В нашем случае правая часть нулевая, поэтому определение принимает более простой вид: схема устойчива, если существует не зависящая от  константа , такая что для любой функции :

Докажем абсолютную устойчивость разностной схемы с помощью этого определения. Используя то, что , оценим:

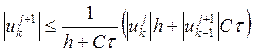
Обозначив , получаем новую оценку решения:

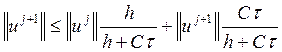
Перенеся слагаемое, содержащее , в левую часть и приведя подобные, получаем:

.

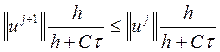Осталось разделить обе части неравенства на . Окончательная оценка такова: . Норма решения на каждом временном слое не превышает нормы решения на предыдущем слое, а на нулевом слое: . Значит, . Определение устойчивости выполняется, т.к. есть не зависящая от  константа .

В случае  устойчивость проверяется точно также.

Для разностной схемы доказана аппроксимация и абсолютная устойчивость. Значит, по теореме сходимости, которая утверждает, что при наличии аппроксимации из устойчивости следует сходимость, решение разностной задачи будет сходиться к решению дифференциальной. Т.е. можем применять поставленную сеточную задачу для нахождения численного решения исходного уравнения.

К-свойство схемы

Протестируем разностную схему на решении, называемом «бегущая ступенька». Для этого зададим несогласованные начальные и краевые условия. Пусть . Уравнения характеристик имеют вид: , вдоль характеристик функция  постоянна. Характеристика  делит область решения на 2 подобласти и является линией, вдоль которой распространяется разрыв функции . Точное решение задачи имеет вид:

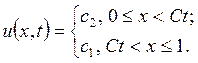
Графически решение представляет собой «ступеньку», бегущую слева направо со скоростью .

Разностные схемы сглаживают разрыв решения при . Свойство схемы не сглаживать разрыв называется К-свойством.

Исследуем неявную схему бегущего счета на наличие К-свойства. Рассмотрим случай , зададим несогласованные начальные и краевые условия: .

При оценке погрешности аппроксимации была получена формула (1). Пусть  - некоторая достаточно гладкая функция. Тогда уравнение:

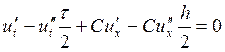                                                               (2)

называется первым дифференциальным приближением разностной схемы. Продифференцируем это уравнение по  и по :

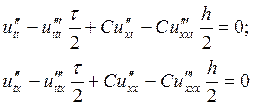
Выразим из этой системы производную , подставим ее в уравнение (2). Пренебрегая членами более высокого порядка малости, чем  и , получим другую форму первого дифференциального приближения разностной схемы:

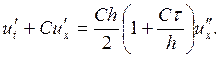                                                                (3)

Наша разностная схема аппроксимирует полученное дифференциальное уравнение второго порядка параболического типа с порядком , а исходное всего лишь с порядком . Т.е. это параболическое уравнение лучше отражает свойства схемы. А его решение – гладкая функция, даже при разрывных начальных данных. Уравнение (3) будет параболическим независимо от соотношения между  и , так как коэффициент при  всегда будет положительным. Поэтому схема будет сглаживать разрыв при любых  и , т.е. К-свойством неявная схема бегущего счета не обладает.

Численные эксперименты

Точное решение

Ищем численное решение разностной задачи при таких начальных и краевых данных:

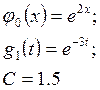
Точное решение дифференциальной задачи в этом случае

		Погрешность решения
0.2	0.2	0.49
0.1	0.1	0.19
0.05	0.05	0.10

Погрешность решения, как и ожидалось, получилась порядка , при уменьшении  и  в 2 раза погрешность тоже уменьшается примерно вдвое.

«Бегущая ступенька»

Протестируем программу на решении, называемом «бегущая ступенька», задавая несогласованные начальные и краевые условия:

 

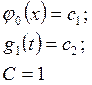
Теоретически погрешность решения должна быть порядка , и не должна сильно зависеть от начальных данных.

Возьмем сначала . В следующей таблице приведены результаты численного эксперимента при разных  и :

		Погрешность решения
1	5	2.00
1	2	0.50
1	1.1	0.05

Погрешность решения получилась очень большая.

Теперь пусть ,  и  будем брать такие же. Теоретически, погрешность должна уменьшится в 2 раза. Но она совсем не изменилась:

		Погрешность решения
1	5	2.00
1	2	0.50
1	1.1	0.05

Дело в том, что неявная схема бегущего счета не обладает К-свойством, т.е. при таких начальных и краевых данных схема всегда сглаживает «ступеньку». Поэтому, несмотря на то, что теоретическая погрешность решения , при тестировании программы на «бегущей ступеньке» погрешность получается порядка половины скачка (разности между  и ).