begin f12:=-2*x[2];
end;
function f21(x:mas):real;
begin f21:=10/x[1];
end;
function f22(x:mas):real;
begin f22:=1;
end;
{Процедура решения системы линейных алгебраических
уравнений (19) методом Гаусса}
Procedure Gauss(var a:mas1;var b,x:mas);
var i,j,k:integer;
c,S:real;
begin
for k:=1 to n-1 do
for i:=k+1 to n do
begin c:=a[i,k]/a[k,k];
a[i,k]:=0;
for j:=k+1 to n do
a[i,j]:=a[i,j]-c*a[k,j];
b[i]:=b[i]-c*b[k];
end;
x[n]:=b[n]/a[n,n];
for i:=n-1 downto 1 do
begin S:=0; for j:=i+1 to n do
S:=S+a[i,j]*x[j];
x[i]:=(b[i]-S)/a[i,i];
end;
end; {GAUSS}
BEGIN for i:=1 to n do
begin
write('Введите начальные приближения x0',i,'=');
readln(x[i]);
end;
ki:=1;
repeat ja[1,1]:=f11(x);
ja[1,2]:=f12(x);
ja[2,1]:=f21(x);
ja[2,2]:=f22(x);
b[1]:=-f1(x);
b[2]:=-f2(x);
Gauss(ja,b,dx);
dxmax:=dx[1];
for i:=1 to n do
begin x[i]:=x[i]+dx[i];
if dxmax<dx[i] then dxmax:=dx[i];
{writeln(' dx',i,'=',dx[i]);}
end;
ki:=ki+1
until abs(dxmax)<e;
for i:=1 to n do
writeln(' x',i,'=',x[i]:7:3);
writeln(' Количество итераций =',ki);
readln;
END.
Задание6
Задание 6 имеет учебной целью закрепление пройденного материала по теме «Обыкновенные дифференциальные уравнения и системы.Задача Коши. Метод Рунге – Кутта».
Условие задания 6. Решить дифференциальное уравнение второго порядка
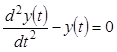 (21)
(21)
с
начальными условиями ![]() ,
, ![]() , при
, при ![]() . Шаг интегрирования
. Шаг интегрирования ![]() , время интегрирования
, время интегрирования ![]() .
.
Алгоритм выполнения задания. Для разработки программы на языке Паскаль введем следующие обозначения. Запишем систему n обыкновенных дифференциальных уравнений (ОДУ) в следующем виде:
 (22)
(22)где х – независимая переменная.
Основная задача, связанная с этой системой, называется задачей Коши, которая предполагает нахождение решения системы ОДУ, удовлетворяющего nначальным условиям
Решение задачи Коши будем находить методом Рунге-Кутта IV порядка. Его расчетные формулы имеют вид
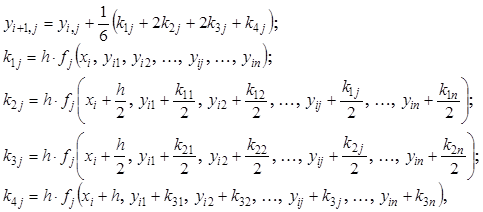 (23)
(23)где
![]() ;
; ![]() .
.
В результате решение получается в виде таблицы.
Для
решения уравнения (21) представим его в форме Коши. Для этого сделаем замену
переменных: ![]() ;
; ![]() . В
результате получим систему двух дифференциальных уравнений первого порядка
. В
результате получим систему двух дифференциальных уравнений первого порядка
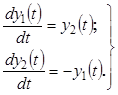 (24)
(24)
Ниже приведен текст программы на языке Паскаль.
Program Runge;
{Решение системы дифференциальных уравнений
методом Рунге-Кутта}
const n=2;
Type mas=array[1..n] of real;
var t0,tk,t,h:real;
j:integer;
y0,y,yp,dy,k1,k2,k3,k4,yk1,yk2,yk3:mas;
{Процедура задания функции правых частей системы (24)}
Procedure F(t:real;y:mas;var yp:mas);
begin yp[1]:=y[2];
yp[2]:=-y[1];
end;
begin t0:=0; tk:=5; h:=0.1;
y[1]:=1; y[2]:=0;
t:=t0;
repeat f(t,y,yp);
for j:=1 to n do begin k1[j]:=h*yp[j];
yk1[j]:=y[j]+k1[j]/2;
end;
f(t+h/2,yk1,yp);
for j:=1 to n do begin k2[j]:=h*yp[j];
yk2[j]:=y[j]+k2[j]/2;
end;
f(t+h/2,yk2,yp);
for j:=1 to n do begin k3[j]:=h*yp[j];
yk3[j]:=y[j]+k3[j]/2;
end;
f(t+h,yk3,yp);
for j:=1 to n do k4[j]:=h*yp[j];
t:=t+h;
write (' t=',t:5:3);
for j:=1 to n do begin
dy[j]:=(k1[j]+2*k2[j]+2*k3[j]+k4[j])/6;
y[j]:=y[j]+dy[j];
write (' y',j,'=',y[j]:6:4);
end;
writeln
until t>tk;
end.
Задание7
Задание 7 имеет учебной целью закрепление пройденного материала по теме «Ряды Фурье. Прямое и обратное преобразование Фурье. Разложение периодического сигнала в ряд Фурье».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.