Нормальное распределение случайной величины. Числовые характеристики нормального распределения

§9. Нормальное распределение случайной величины. Числовые характеристики нормального распределения

Если вид кривой описывается формулой 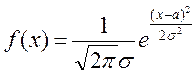, то распределение случайной величины называется нормальным. Данную функцию называют функцией Гаусса. Графиком нормального распределения является колокол симметричный относительно центра распределения.

Часто возникают распределения, хотя и не отвечающие строго нормальному распределению, но имеющие с ним сходство. Такие сходные черты часто обусловлены тем, что крайние значения вариантов, близкие к X_min и Х_mах, встречаются много реже, чем серединные.

Нормальное распределение имеет два признака:

1. Чем дальше от центра, тем ниже опускаются ветви графика, что свидетельствует о снижении вероятности появления случайной величины, при сильном отклонении ее от центрального значения.

2. График симметричен относительно центра, что говорит о равных вероятностях появления значений случайной величины  как слева от центра, так и справа от него. Вспомните формулу P_i=f_i∆x_i.Если график разбить на неширокие интервалы, в пределах которого плотность вероятности остается почти постоянной величиной, то  нетрудно понять, что вероятность равна площади S, откуда и следует равенство вероятностей при равенстве площадей. P=S!

Рис. 9.1

В формулу Гаусса входят две величины, которые являются  числовыми характеристиками случайной величины  или параметрами случайной величины. От их значения зависит вид графика распределения. Одной из задач математической статистики является нахождение, указание данных параметров случайной величины.

Первый параметр, обозначаемый  как а, называется математическим ожиданием. Он характеризует центр распределения случайной величины. Для  нахождения математического ожидания используется формула , где  х_i - значение случайной величины  – роста, веса и т.д.,  p_i - вероятность появления значения случайной величины. Если учесть, что 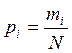 , то получим формулу 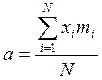, из которой видно, что математическое ожидание – это среднее значение случайной величины  во всей ее генеральной совокупности. Из графика видно, что при х=а кривая имеет максимум. Математическое ожидание в медицинских и биологических исследованиях принято называть нормой показателя или истинным значением.

Другой числовой характеристикой случайной величины является дисперсия, обозначаемая буквой D или σ² (D=σ²). 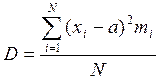, где N объем генеральной совокупности. Эта величина отражает меру рассеяния значений случайной величины возле центра распределения. Одни значения случайной величины сильнее отличаются от центра, другие меньше. Чтобы оценить степень отклонения любого значения случайной величины от центра (от математического ожидания), а иначе говоря, оценить  среднее отклонение, нужно все отклонения (x_i – a) сложить и разделить на число испытаний.

Но поскольку для нормального распределения все отклонения равновероятны, то получим нуль, т.к. отклонения слева от центра отрицательны, а справа - положительны.

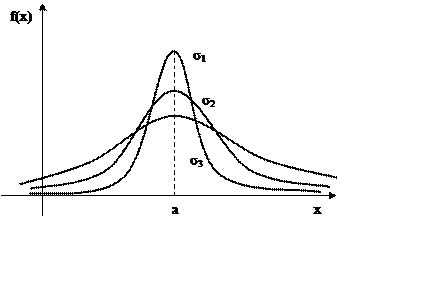
Рис. 9.2

Чтобы этого не случилось, отклонения приходится возводить в квадрат. Т.о. дисперсия будет иметь размерность случайной величины, но только в квадрате. Чтобы избавиться от этого «неудобства» приходится извлекать корень квадратный из дисперсии.  Очевидно, что величина, произведенная от дисперсии, также  характеризует разброс или рассеяние значений случайной величины вокруг центра. Корень квадратный из дисперсии  называется   средним квадратичным отклонением (с.к.о.) или стандартным отклонением и обозначается буквой σ (), тогда

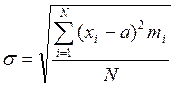
Когда параметр σ уменьшается, ордината f(x) кривой растет. Подъем кривой в центральной части компенсируется более резким спадом ее к оси 0х, так что общая площадь остается неизменной и равной единице P=S=1.  На рис. 9.2 приведены графики с одним математическим ожиданием, но  разным разбросом.

Теоретически случайная величина распределенная по нормальному закону, может принимать любые значения от –∞ до +∞.  На самом деле, как видно из графика, плотность вероятности по мере удаления от центра быстро убывает и при х = а ± 3σ  значениями плотности вероятности можно пренебречь.

Графики распределения продолжительности жизни мужчин и женщин относятся к нормальному распределению, однако числовые характеристики этих распределений различны, поэтому графики будут отличаться друг от друга (рис. 9.4). Известно, что средняя  продолжительность женщин выше у женщин, поэтому график будет сдвинут левее по числовой оси.

Рис. 9.3

Известно также, что среди мужчин по разным причинам (войны, бытовые конфликты, суицид и т.д.) жизнь может оборваться в раннем возрасте, а с другой стороны  среди мужчин по сравнению с женщинами встречаются долгожители, намного пережившие средний возраст. Таким образом, разброс будет  выше у мужчин, а, значит, их график будет шире, но ниже, поскольку площадь, равная вероятности, должна быть одинаковой и равной единице.

Рис. 9.4