Приближение времени релаксации, как мы видели, описывает быстрые
процессы, происходящие за времена порядка времени свободного пробега. Существует еще
один способ упрощений кинетического уравнения Больцмана, позволяющий рассмотреть
некоторые важные вопросы кинетики. Этот подход позволяет описать медленные
процессы. Уточним, прежде всего, понятие, медленных процессов. Под медленными процессами в
кинетике подразумевают процессы, в которых средние изменения величин при
каждом акте рассеяния мало меняются по сравнению с их характерными значениями. Пусть τм — время релаксации
таких процессов, тогда процесс является
медленным, если выполнено неравенство следующего типа τ<t*<тм. За время t* происходят акты
рассеяния,
приводящие, однако, к малому изменению параметров. Рассмотрим, например, релаксацию
функции распределения f(![]() , t) при переходах
, t) при переходах ![]() , где
, где ![]() =
=![]() , причем
, причем ![]() <<
<<![]() (отметим, что степень неравновесности
считается произвольной). Входящую в интеграл столкновений функцию распределения f(
(отметим, что степень неравновесности
считается произвольной). Входящую в интеграл столкновений функцию распределения f(![]() , t) можно разложить в
ряд Тейлора по
, t) можно разложить в
ряд Тейлора по ![]() :
:
![]() =
= ![]() +
+ 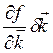 +
+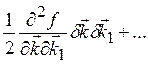 (1.30)
(1.30)
Подставляя (1.30) в (1.4), получаем
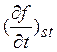 =
= ![]() [
[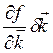 +
+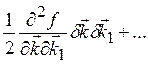 ]d
]d![]() =
=
![]()
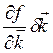 d
d![]() +
+![]()
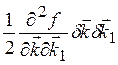 d
d![]() (1.31)
(1.31)
Отсюда сразу следует
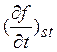 =
=
![]() f
f ![]()
![]() d
d![]() +
+ 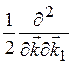 f
f ![]()
![]() d
d![]()
Вводя обозначения
![]() =
=![]()
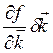 d
d![]() (1.32)
(1.32)
![]() =
= ![]()
![]()
![]() d
d![]() (1.33)
(1.33)
получаем
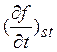 =
= ![]() [
[![]()
![]() +
+ ![]()
![]()
![]() ] (1.34)
] (1.34)
В отсутствие внешних сил однородное кинетическое уравнение с учетом (1.34) записывается в виде
![]() =
= ![]() [
[![]()
![]() +
+ ![]()
![]()
![]() ] (1.35)
] (1.35)
Заметим, что
физический смысл величин ![]() и
и ![]() нетрудно
понять, если записать их ,в
виде
нетрудно
понять, если записать их ,в
виде 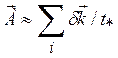 ,
, 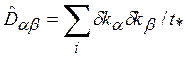
Здесь ![]() — характерное изменение импульса в одном
акте рассеяния.
Суммирование происходит по большому числу актов столкновении за время t* ,. Таким образом,
коэффициенты уравнения (1.35) выражаются через осредненные по многим ,актам рассеяния
характеристики.
— характерное изменение импульса в одном
акте рассеяния.
Суммирование происходит по большому числу актов столкновении за время t* ,. Таким образом,
коэффициенты уравнения (1.35) выражаются через осредненные по многим ,актам рассеяния
характеристики.
Уравнение (1.35),
позволяет ввести величину плотности тока'в импульсном или ![]() пространстве
пространстве
![]() = -
= - ![]()
![]() -
- ![]()
![]()
![]() (1.36)
(1.36)
С помощью последнего
соотношения уравнение (1.35) можно записать в виде закона сохранения—уравнения
неразрывности в ![]() -пространстве:
-пространстве:
![]() +
+ ![]() = 0 (1.37)
= 0 (1.37)
Отметим, что можно
провести формальную аналогию с гидродинамикой: величины ![]() есть компоненты средней (конвективной) скорости фазовых точек в
есть компоненты средней (конвективной) скорости фазовых точек в ![]() -пространстве, компоненты
Dαβ, есть компоненты тензора диффузии в этом пространстве.
Следовательно, уравнения (1.35) или (1.37)
-пространстве, компоненты
Dαβ, есть компоненты тензора диффузии в этом пространстве.
Следовательно, уравнения (1.35) или (1.37)
описывают процесс
диффузии в ![]() -пространстве. Аналогично можно рассмотреть эволюцию функции
распределения в энергетическом
пространстве, когда энергия системы мало меняется в каждом отдельном акте взаимодействия (см. подробнее [2]). Ясно, что таким же способом можно изучить медленные процессы в обычном — координатном —
пространстве. Уравнения, описывающие
медленную эволюцию функций распределения
в координатном, импульсном или энергетическом пространстве типа (1.35) или (1.37), носят название уравнений Фоккера—Планка. Приближение, лежащее в основе их получения, называют диффузионным. Процессы,
описываемые этим приближением,
весьма многочисленны: обычные диффузия
и теплопроводность, броуновское движение, диффузия нейтронов в среде, кинетика металлов при низких
температурах и т. д. (примеры можно
найти в [2]).
-пространстве. Аналогично можно рассмотреть эволюцию функции
распределения в энергетическом
пространстве, когда энергия системы мало меняется в каждом отдельном акте взаимодействия (см. подробнее [2]). Ясно, что таким же способом можно изучить медленные процессы в обычном — координатном —
пространстве. Уравнения, описывающие
медленную эволюцию функций распределения
в координатном, импульсном или энергетическом пространстве типа (1.35) или (1.37), носят название уравнений Фоккера—Планка. Приближение, лежащее в основе их получения, называют диффузионным. Процессы,
описываемые этим приближением,
весьма многочисленны: обычные диффузия
и теплопроводность, броуновское движение, диффузия нейтронов в среде, кинетика металлов при низких
температурах и т. д. (примеры можно
найти в [2]).
Для иллюстрации применения уравнения Фоккера—Планка рассмотрим броуновское движение частицы в среде под действием внешней силы. В этом случае следует несколько обобщить уравнение (1.35) с учетом внешних сил. Для простоты изучим одномерный случай движения частицы под действием силы Fи случайных толчков со стороны среды. Пусть средняя скорость частицы связана с действующей силой соотношением v = μF(μ, называется коэффициентом подвижности); подобная связь имеет место, например, в законе Ома. Уравнение Фоккера—Планка с учетом этого соотношения запишется в виде
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.