Кинетическая теория процессов переноса и поверхностных явлений в твёрдом теле, страница 2

Вероятности переходов Wсвязаны с эффективным сечением рассеяния. Например, если рассеяние квазичастиц происходит на неподвижном силовом центре (в этом случае состояние рассеивателя предполагается неизменным), применимо соотношение (1.4) и эта связь имеет вид                           

=                                                                                                                                             (1.9)

Напомним, что дифференциальное эффективное, сечение есть число квазичастиц, рассеянных в единицу времени в телесный угол dΩ, деленное на число квазичастиц, проходящих в единицу времени через единичную площадку: , где θ, φ — углы рассеяния в сферической системе координат. При этом dQ = ,  v_oth =  , — скорости квазичастиц до столкновений. Подставляя (1.9) в (1.5), получим

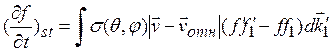     (1.10)

где (введены обозначения ,  и т. д. Таким образом, задача вычисления ивтепрала столкновений 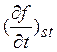 сводится в первую очередь к определению дифференциального эффективного сечения а .

1.3. Сечение рассеяния

Определение дифференциального эффективного сечения рассеяния составляет задачу механики (классическую или квантовую). Напомним некоторые относящиеся сюда факты, связанные с вычислением в квантовой механике (подробнее см. в [3, 4]).

При рассеянии на неподвижном силовом центре сечение рассеяния в изотропном случае связано в борновском приближении с амплитудой рассеяния формулой

                               (1.11)

где

А (θ)= - 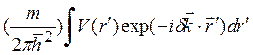                                (1.12)

При этом

А (θ) ~  =  ~                            (1.12)

Здесь —матричный элемент перехода из состояния k(до рассеяния) в состояние k' (после рассеяния) под действием потенциала рассеивателя V(r). Полное (интегральное) сечение рассеяния находится как

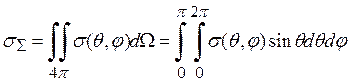                                                                        (1.13)            

В изотропном случае  не зависит от угла φ. Тогда имеем

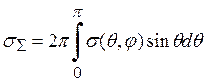                                                   (1.14)

Если σ не зависит от θ, то . В том случае, когда радиус действия сил рассеивающего центра ~r₀, величину σ можно оценить как σ ~ r₀².

. Введем понятие о длине свободного пробега l — среднего расстояния, проходимого квазичастицей между двумя последовательными столкновениями. Если N — число рассеивающих центров, то величина l~ l/Nσ~ 1/Nr₀². Число N~r^-3 (r—среднее расстояние между рассеивателями). Тогда получаем

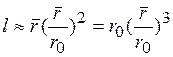                                (1.15)

Поскольку r>>r₀, то l>>r. Здесь можно также ввести понятие о времени свободного пробега r~l/v     (v— средняя скорость квазичастиц). Приведенные оценки будут использованы ниже для оценок величин кинетических коэффициентов.

1.4. Приближение времени релаксации

Полученное выше уравнение Больцмана с интегралом столкновений, выраженным через экспериментально измеряемую величину — эффективное сечение рассеяния, — является нелинейным мнтегро-дифференциальным уравнением, (решить которое в общем виде не представляется возможным. Существуют, однако, методы, позволяющие . упростить интеграл столкновений и тем самым получить решение этого уравнения. Первое приближение описывает быстрые процессы, происходящие за времена ~ времени свободного пробега (или времени релаксации). Второе приближение, которое будет рассмотрено в следующем разделе, описывает медленные процессы (диффузионное приближение), происходящие при малом изменении параметров, входящих в функцию распределения, за время свободного пробега.

Рассмотрим сначала приближение, носящее название приближения времени релаксации (или τ — приближения).

Последнее приближение справедливо, если расамаггриваютюя неравновесные состояния, которые не слишком далеки от состояния термодинамического равновесия. Кроме этого, как будет видно, так можно рассматривать лишь те процессы, где основную роль илрает упругое рассеяние. При этом энергия квазичастиц до и после столкновений постоянна ε=ε', , изменяется только направление . Реально отмеченные условия соответствуют многим задачам физической кинетики (подробнее τ — приближение обсуждается в [1, 2,6])