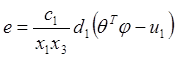Air to fuel ratio and torque control of spark ignition engines, страница 3

.                                                                      (19)

Analysis of the error model (19) motivates the following structure of adaptive controller

                                                                                            (20)

where the vector of adjustable parameters  is generated by the adaptation algorithm with improved parametric convergence [6].

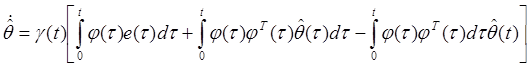                                    (21)

with gain function

,  

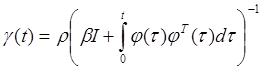where  is a small constant.

Taking (20) in (19) and transforming equation (21) we obtain the parametric error  and stabilization error  models of the closed loop system:

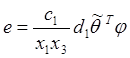,                                                                               (22)

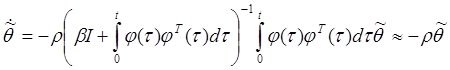.               (23)

Thus adaptive control law proposed is described by equations (21):

(13), (14) – state observer;

(20) – adjustable controller;

(21) – adaptation algorithm.

Properties of the closed loop system are established by the following proposition: for any  and any initial conditions all the signals in the closed loop system consisting of the plant (7), (9), state observer (13), (14) adjustable controller (20) and adaptation algorithm (21) are bounded and additionally  as  asymptotically if elements of matrix 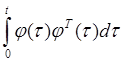 are linearly independent. Moreover the rate of parameter convergence and the speed of the closed-loop system can be arbitrary increased with increasing parameter  that results from equation (23).

Remark 2: In spite of perfect convergence some integrals in the expression (21) grow unboundly as . Therefore in practice resetting of integration in definite time period has to be used

3. Nonlinear torque control

At the stage of torque control synthesis we assume that engine parameters , ,  are determined in the course of experiment and a priory known.

To provide asymptotic convergence of indicated torque according to expression (12) let us define the reference signal  using equation (10) as

                                                          (24)

where  is the reference signal of air pressure in the intake manifold. Let us express  as

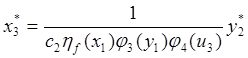.                                                        (25)

Now we introduce error signal  where  is the state variable of reference model

, .                                                         (26)

Let us define the error model as

                                                                                          (27)

that provides asymptotic tracking of signal . Assuming that the subsystem described by equation (6) is stable (i.e. engine works at stable regimes) and analyzing error model (27) we obtain the following control law:

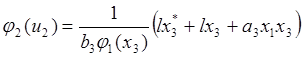                                                          (28)

or

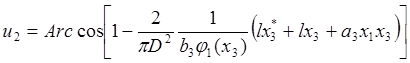.                                   (29)

Thus the torque regulator is presented by equations (25) and (29).

For any  and any initial conditions all the signals in the closed loop system consisting of the stable plant (6), (8), (10) and regulator (25), (29)  as  asymptotically.

4. Simulation

To confirm validity of engine model and illustrate the work of closed loop system MathLab/ Simulink software is used. Engine parameters and approximations of static functions of the engine (Ford 840 Ci, motronic) model are presented in tables 1 and 2 [10]. Parameters of air to fuel ratio controller (13), (14), (20), (21) and torque controller (25), (29) are presented in table 3.

Table 1. Engine parameters.                                                 Table 2. Static functions.