ПРИМЕРЫ. а) ![]() – линейное
неоднородное дифференциальное уравнение третьего порядка с переменными
коэффициентами;
– линейное
неоднородное дифференциальное уравнение третьего порядка с переменными
коэффициентами;
б) ![]() – линейное однородное дифференциальное
уравнение второго порядка с постоянными коэффициентами;
– линейное однородное дифференциальное
уравнение второго порядка с постоянными коэффициентами;
в) ![]() – нелинейное дифференциальное
уравнение второго порядка.
– нелинейное дифференциальное
уравнение второго порядка.
Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка
![]() , (10.11)
, (10.11)
![]() .
.
Уравнение
![]() (10.12)
(10.12)
называется
однородным дифференциальным уравнением, соответствующим линейному неоднородному
уравнению (10.11). Это уравнение имеет решение ![]() ,
которое называется нулевым или тривиальным.
,
которое называется нулевым или тривиальным.
ТЕОРЕМА 1 (о
линейной комбинации решений линейного однородного дифференциального
уравнения). Пусть ![]() – два решения линейного
однородного дифференциального уравнения (10.12). Тогда для любых постоянных
– два решения линейного
однородного дифференциального уравнения (10.12). Тогда для любых постоянных ![]() линейная комбинация
линейная комбинация ![]() также является решением (10.12).
также является решением (10.12).
Доказать самостоятельно.
ПРИМЕР. Рассмотрим
уравнение ![]() . Легко проверить непосредственной подстановкой,
что функции
. Легко проверить непосредственной подстановкой,
что функции ![]() – его решения.
– его решения.
По
теореме 1 при любых ![]() функция
функция
![]()
– решение этого дифференциального уравнения.
Функция ![]() тоже является решением.
тоже является решением.
ОПРЕДЕЛЕНИЕ. Два решения однородного дифференциального уравнения (10.12) называются линейно независимыми, если их отношение постоянно. В противном случае эти решения называются линейно независимыми.
ПРИМЕР. Для решений уравнения из предыдущего примера имеем:
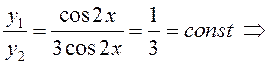
![]() – линейно зависимы;
– линейно зависимы;
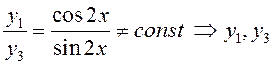 – линейно
независимы;
– линейно
независимы;
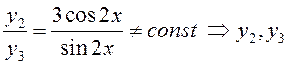 – линейно
независимы.
– линейно
независимы.
ОПРЕДЕЛЕНИЕ.
Определителем Вронского ![]() функций называется
функциональный определитель вида
функций называется
функциональный определитель вида
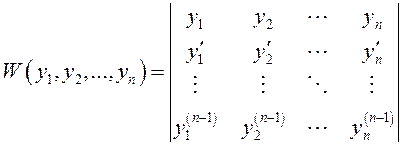 .
.
Для
двух функций определитель Вронского имеет вид 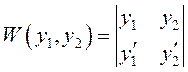 .
.
ПРИМЕР. Для рассмотренных выше решений
 ;
; 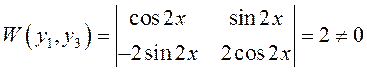 .
.
ТЕОРЕМА 2 (о
необходимом и достаточном условии линейной зависимости решений
линейного однородного дифференциального уравнения). Пусть ![]() непрерывны, а
непрерывны, а ![]()
![]() . Тогда для того, чтобы решения
. Тогда для того, чтобы решения ![]() дифференциального уравнения (10.12) были линейно
зависимы на
дифференциального уравнения (10.12) были линейно
зависимы на ![]() , необходимо и достаточно, чтобы
определитель Вронского
, необходимо и достаточно, чтобы
определитель Вронского ![]() был равен нулю хотя бы
для одного значения
был равен нулю хотя бы
для одного значения ![]() .
.
ДОКАЗАТЕЛЬСТВО.
1.
Необходимость: решения ![]() линейно зависимы
линейно зависимы ![]() хотя бы при одном значении
хотя бы при одном значении ![]() .
.
По
определению линейной зависимости двух решений 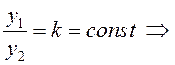
![]()
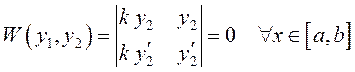 .
.
2. Достаточность: ![]() решения
решения
![]() дифференциального уравнения (10.12) линейно
зависимы.
дифференциального уравнения (10.12) линейно
зависимы.
Так как (10.12) – линейное однородное дифференциальное
уравнение, то оно имеет нулевое решение ![]() , для
которого
, для
которого ![]() .
.
Рассмотрим систему линейных алгебраических уравнений
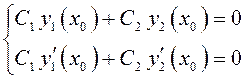 . (10.13)
. (10.13)
Ее
основной определитель ![]() по условию, поэтому она имеет
бесконечное множество решений (см.гл.1). Пусть
по условию, поэтому она имеет
бесконечное множество решений (см.гл.1). Пусть ![]() – некоторое
нетривиальное решение (10.13). Тогда функция
– некоторое
нетривиальное решение (10.13). Тогда функция ![]() по
теореме 1 – решение (10.12), причем вследствие (10.13)
по
теореме 1 – решение (10.12), причем вследствие (10.13) ![]() .
.
Таким образом, одним и тем же начальным условиям
удовлетворяют два решения уравнения (10.12), что противоречит теореме Коши. Следовательно,
![]()
 , то есть решения
, то есть решения ![]() линейно зависимы.
линейно зависимы.
Что и требовалось доказать.
ЗАМЕЧАНИЕ.
Для линейной зависимости ![]() решений линейного однородного
дифференциального уравнения
решений линейного однородного
дифференциального уравнения ![]() -го порядка необходимо и
достаточно, чтобы их определитель Вронского был равен нулю хотя бы в одной
точке.
-го порядка необходимо и
достаточно, чтобы их определитель Вронского был равен нулю хотя бы в одной
точке.
ТЕОРЕМА 3 (о
структуре общего решения линейного однородного дифференциального уравнения
второго порядка). Пусть ![]() непрерывны
непрерывны ![]() ,
, ![]() и
и ![]() – произвольные линейно независимые решения
дифференциального уравнения (10.12). Тогда общее решение этого уравнения имеет
вид:
– произвольные линейно независимые решения
дифференциального уравнения (10.12). Тогда общее решение этого уравнения имеет
вид:
![]() .
.
ДОКАЗАТЕЛЬСТВО.
По теореме 1 ![]() – решение (10.12)
– решение (10.12) ![]() . Покажем, что оно общее.
. Покажем, что оно общее.
Зададим произвольные
начальные условия ![]() , удовлетворяющие условиям
теоремы Коши. Тогда для определения постоянных
, удовлетворяющие условиям
теоремы Коши. Тогда для определения постоянных ![]() получим
систему линейных алгебраических уравнений
получим
систему линейных алгебраических уравнений
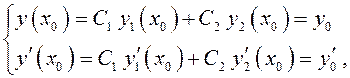
основной
определитель которой ![]() по теореме 2.
по теореме 2.
Значит,
система имеет единственное решение ![]() , а функция
, а функция ![]() – решение дифференциального уравнения (10.12),
удовлетворяющее заданным начальным условиям.
– решение дифференциального уравнения (10.12),
удовлетворяющее заданным начальным условиям.
Таким образом, ![]() по
определению – общее решение дифференциального уравнения (10.12).
по
определению – общее решение дифференциального уравнения (10.12).
Что и требовалось доказать.
ПРИМЕР.
Ранее были найдены линейно независимые решения дифференциального уравнения ![]() . Теперь можно записать общее
решение этого уравнения:
. Теперь можно записать общее
решение этого уравнения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.