Дифференциальные уравнения. Элементы теории устойчивости: Конспект лекций (Системы дифференциальных уравнений. Устойчивость решений систем дифференциальных уравнений)

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Омский государственный технический университет»

Н.И. Николаева

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ

Конспект лекций

Часть 5

Омск

Издательство ОмГТУ

2011

УДК

ББК

Рецензенты:

Ю.Ф.Стругов, д-р физ.-мат. наук;

С.Е.Макаров, канд. физ.-мат. наук, доцент

Николаева Н.И.

Дифференциальные уравнения. Элементы теории устойчивости. Конспект лекций. Часть 5 / Н.И. Николаева. – Омск: Изд-во ОмГТУ, 2011. –  88 с.

Пособие представляет собой конспект лекций, читаемых автором  на втором  курсе технического университета, и предназначено для студентов всех форм обучения. 

Часть 5 включает в себя три  главы: «Дифференциальные уравнения», «Системы дифференциальных уравнений» и «Устойчивость решений систем дифференциальных уравнений». Изложение сопровождается достаточным количеством примеров, поясняющих наиболее важные теоретические положения, иллюстрирующих  теоретический материал и дающих образцы решения задач.

Автор благодарит доцента кафедры Высшей математики ОмГТУ Лореша М.А., который внимательно прочел рукопись. Его советы и замечания немало способствовали улучшению текста. Автор также выражает признательность А.Лымарю и зав.методическим кабинетом кафедры Царицинской Т.Г. за большую помощь в техническом оформлении рукописи.

Печатается по решению редакционно-издательского совета

Омского государственного технического университета

Оглавление

Глава 10.  ДИФФЕРЕНЦИАЛЬНЫЕ  УРАВНЕНИЯ

 10.1. Основные определения и примеры

При решении многих задач математики, физики и механики часто не удается установить непосредственную зависимость между искомыми и данными переменными величинами, но зато удается составить уравнение, связывающее независимую переменную, искомую функцию и ее производные. Такое уравнение называется дифференциальным.

ПРИМЕР.  Тело охладилось за 10 минут от 100С до 60С. Температура окружающего воздуха поддерживается постоянной и равной 10С. Определить через сколько минут температура тела станет равной 20С.

Как известно из физики, скорость охлаждения пропорциональна разности между температурой тела и температурой окружающей среды.

Обозначим  – температуру тела в некоторый момент времени . Тогда скорость изменения температуры равна производной , и поэтому данный физический процесс описывается уравнением 

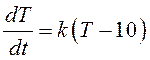                               ,                                         (10.1)

где  – коэффициент пропорциональности, подлежащий определению. Это уравнение является дифференциальным. Искомая функция должна удовлетворять условиям  задачи, а именно,

ПРИМЕР. Гибкая однородная нить подвешена за два конца. Найти уравнение кривой, по которой расположится нить под действием собственного веса (такую форму имеют подвешенные канаты, провода, цепи, поэтому уравнение этой кривой называется уравнением цепной линии).

Пусть  – самая низкая точка нити, а  – произвольная точка. Часть  находится в равновесии под действием трех сил (рис.1):  1) сила натяжения  , направленная по касательной в точке   и составляющая  угол  с осью , 2) сила натяжения в точке ,  действующая горизонтально, 3) вес , приложенный в центре масс и направленный вниз, , где  – линейная плотность,  – длина дуги.