Игровая задача в центральном поле ньютоновского тяготения

Санкт-Петербургский государственный университет

Факультет прикладной математики - процессов управления

Салахиева

Марина

Рафиковна

Группа    452__

Практическая работа по дисциплине

«Моделирование социально-экономических систем.»

Тема: «Игровая задача в центральном поле ньютоновского тяготения»

Преподаватель Малафеев О. А.

Санкт-Петербург

2010

Рассматриваются управляемые космические аппараты (КА) с солнечными парусами (СП) на кеплеровских орбитах. Управление полетом КА осуществляется путем изменения угла установки СП относительно солнечных лучей. Будем считать, что в начальный момент времени КА уже выведены на свои орбиты и им задана начальная скорость.

1. Рассмотрим аппроксимирующие многошаговые игры (х_0, у₀, Т) верхнюю и (х₀, у₀,Т) нижнюю. Здесь х_0, у₀ – начальные кеплеровские орбиты игроков Е и Р соответственно;  Т-продолжительность игры; δ – разбиение интервала [0, T] на n интервалов.

Игра (х₀, у₀,Т) протекает следующим образом. На первом шаге в момент t₀ = 0 игрок Е находясь в начальной позиции х₀, выбирает угол установки СП γ_х⁰, t[t₀,t₁], а игрок Р, зная выбор игрока Е, выбирает угол установки СП γ_у⁰, t[t₀,t₁]. В результате чего в соответствии с динамикой игроки переходят к моменту t₁=T/n в состояния х₁, у₁. На втором шаге в момент t₁ игрок Е, зная предыдущие выборы обоих игроков, выбирает угол установки СП γ_х¹, t[t₁,t₂], а игрок Р, зная сверх того последний выбор игрока Е, выбирает угол установки СП γ_у¹, t[t₁,t₂], в результате чего игроки переходят к моменту t₂ в состояния х₂, у₂. На последнем n – м шаге в момент Т игра заканчивается и игрок l = P , E получает свой выигрыш : величину H_l(). H_l – непрерывная функция игрока l,  положения КА Е и Р соответственно, на орбите в конечный момент времени Т.

Игра (х_0, у₀, Т) протекает двойственным образом : очередность игроков на каждом шаге меняется.

Пусть Н(= ρ()

На пространстве позиции игры  введем функцию расстояния следующим образом:

     

 - положения КА Е и Р соответственно, на орбите в момент времени t.

Целью игрока Е является уклонение от игрока Р к моменту окончания игры на максимальное расстояние. Цель игрока Р – максимальное сближение с игроком Е к моменту окончания игры Т.

Позиция игры есть пара f = (f_p, f_E), где f_Е = (x ,γ_х ),  f_р = (y , γ_у) , их множество обозначим через F  = F_p×F_E, где, в свою очередь, F_p, F_E – множества позиций игроков Р и Е соответственно.

Стратегия φ_р (φ_Е) игрока Р (Е) в игре (^.) есть правило, ставящее в соответствие состоянию игры  угол установки СП, а соответственно вектор импульса. Множество всех стратегий Р (Е) обозначим через Ф_р (Ф_Е).

Для решения игры применяем метод динамического программирования. Введем функцию Н(х₀, у₀, Т) (для нижней игры). Её значение в точке  (х₀, у₀, Т) положим равным

Н(х₀, у₀, Т) = , где  - конечное положение КА в ситуации выбора пары стратегий (φ_р, φ_Е) = φ (в конечной точке траектории игры χ(φ) ).

Здесь под траекторией игры понимаем последовательность позиции игры в ситуации φ с начальной позицией f ⁰.

Справедливы следующие соотношения динамического программирования для функции Н(^.) :

Н(х₀, у₀, t₀) = 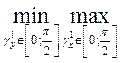Н(х₁, у₁, t₁)

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Н(х_i, у_i, t_i) = 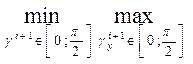Н(х_i+1, у_i+1, t_i+1)                  (1)

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Н(х_n-1, у_n-1, T-δ) =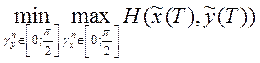

Здесь 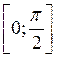 область допустимых углов установки СП.

Утверждение1 [1]. В играх ,  при всяких δ существуют ситуации равновесия в чистых стратегиях.

Доказательство. Проводится аналогично доказательству для утверждения 10.5.8 описанному в [1].

Нахождение функции Н(^.)  значения игры (^.)  и оптимальных стратегий φ_р, φ_Епроводится следующим образом. Сначала находим значение функции Н(х₀, у₀, Т) для всех допустимых орбит х₀, у₀ и значения γ_у, γ_х . Затем с помощью соотношений (1) находим значения Н(^.) для допустимых состояний z = (х₀, у₀), γ_у, γ_х и т.д.

Процесс заканчивается когда построим все значения функций Н(^.), с помощью них и выбранных  γ_у, γ_х последовательно вычисляются значения оптимальных управлений игроков.

2. Уравнение движения КА с СП описывается системой дифференциальных уравнений.

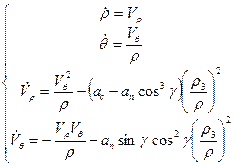
где 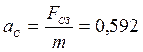см/сек² — гравитационное ускорение Солнца   на орбите Земли; 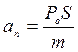(см/сек²) ускорение аппарата, создаваемое парусом, –расстояние от Солнца до орбиты Земли  =149,6^.10⁶км.

Тогда уравнения движения игроков Р и Е задаются следующим образом :

Е :

, , , .

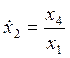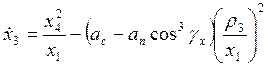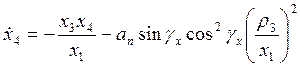Р :

, ,  ,  .

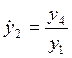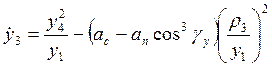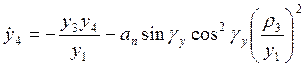Задаем начальные положения КА в виде (ρ; θ; V_ρ, V_θ).

Е : х₀ = (1,6^.10⁸; π/4 ; 4; 0,8)

a_n= 0.12 см/сек².

P:

y₀ = (1,495^.10⁸; π/6; 5; 0,2)  

a_n= 0.22 см/сек².

T = 287 суток. Интервал времени [0;T] разбиваем на n = 100 частей, δ = 2,87 сут.

Вычисления реализованы с помощью математического пакета MatLab 7.6.0.

Результат нижней игры при указанных параметрах :

1) Расстояние ρ в последний момент времени Т :

ρ= 2.4753^.10²⁰км.

2) Выбранные углы (в радианах)

Для Р γ_у :

0.7854    0.7854    0.7854    0.7854    0.7854    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708    1.5708     1.5708    1.5708    1.5708    1.5708      1.5708   0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854   0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854    0.7854