Следует отметить частные постановки задачи идентификации, когда определяют не математическую модель, а некоторые свойства ОУ, например, такие как линейность, стационарность, наличие чистого запаздывания.
Существуют два подхода, на которых базируются алгоритмы идентификации. В первом случае предполагается предварительный сбор информации об объекте с дальнейшей ее обработкой, причем место сбора и обработки могут быть разнесены. Алгоритмы, базирующиеся на таком подходе, называют ретроспективными. Если же искомые параметры и характеристики определяются по мере поступления априорной информации, в так называемом пошаговом режиме, то алгоритмы называют рекуррентными. Рекуррентные алгоритмы используются, например, при идентификации нестационарных объектов или при необходимости уточнения найденных оценок параметров в стационарных объектах.
Процесс идентификации может осуществляться в пошаговом режиме и без поступления новой априорной информации. Такие процессы называют итерационными.
3. ИДЕНТИФИКАЦИЯ ИМПУЛЬСНОЙ
И ЧАСТОТНЫХ ХАРАКТЕРИСТИК
В этом разделе речь пойдет о непараметрической идентификации. Математическая модель линейного динамического объекта в данном случае представляется интегральным уравнением свертки (1.7), решение которого, вообще говоря, является некорректной задачей.
3.1. Решение уравнения свертки посредством преобразования Фурье
Ставится
задача идентификации ИХ ![]() линейного динамического
объекта, представляющая собой решение интегрального уравнения свертки (1.7).
линейного динамического
объекта, представляющая собой решение интегрального уравнения свертки (1.7).
Известно, что свертке (1.6) в частотной области соответствует произведение
![]() , где
, где ![]() и
и
![]() - комплексные спектры входного
- комплексные спектры входного ![]() и выходного
и выходного ![]() сигналов
объекта, а
сигналов
объекта, а ![]() - его АФХ.
- его АФХ.
Методику решения задачи идентификации поэтапно можно представить в следующем виде.
1.
Определяется комплексный спектр сигнала ![]()
![]() .
.
![]() -
оператор прямого преобразования Фурье.
-
оператор прямого преобразования Фурье.
2.
Определяется комплексный спектр сигнала ![]()
![]() .
.
3. Вычисляется комплексная АФХ
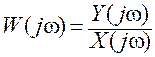 .
.
4. Посредством обратного преобразования Фурье определяется ИХ
![]() .
.
Преобразование
Фурье предполагает финитность, преобразуемых функций, т.е. ![]() ,
, ![]() ,
, ![]() .
.
Если
сигнал ![]() не зашумлен помехой
не зашумлен помехой ![]() , то скорость убывания к нулю комплексного
спектра
, то скорость убывания к нулю комплексного
спектра ![]() при
при ![]() выше,
чем
выше,
чем ![]() в силу того, что
в силу того, что ![]() >
>![]() и условие
и условие ![]() выполняется.
В противном случае, когда имеем
выполняется.
В противном случае, когда имеем ![]() , то
, то ![]() и оценка
и оценка
![]()
может
сколь угодно сильно отличаться от истиной ИХ ![]() , т.е.
решение будет неустойчивым.
, т.е.
решение будет неустойчивым.
3.2. Решение уравнения свертки посредством квадратурных формул
Если
в уравнении свертки (1.6) заменить интеграл квадратурной формулой, то ![]() ,
, ![]() ,
, ![]() . При этом
. При этом ![]()
![]()
![]() и дискретный аналог
выражения (1.6) примет вид
и дискретный аналог
выражения (1.6) примет вид
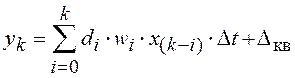 ,
,
![]() и
и ![]() - коэффициенты и погрешность квадратурной
формулы, соответственно.
- коэффициенты и погрешность квадратурной
формулы, соответственно.
Запишем последнее выражение в усеченном виде
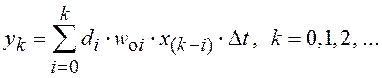 , где
, где ![]() -
оценка ИХ
-
оценка ИХ ![]() . Тогда при
. Тогда при ![]() имеем
имеем
![]() , откуда
, откуда
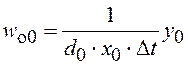 .
.
При ![]()
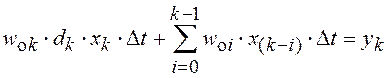
и
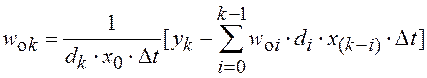 .
.
Полученное
решение будет неустойчивым, так как обычно ![]() . Кроме
того, с увеличением
. Кроме
того, с увеличением ![]() возрастает погрешность
квадратурной формулы
возрастает погрешность
квадратурной формулы ![]() , и, поскольку решение
определяется посредством рекуррентной процедуры, накапливается вычислительная
погрешность. Таким образом, и в данном случае решение задачи идентификации являться
некорректным.
, и, поскольку решение
определяется посредством рекуррентной процедуры, накапливается вычислительная
погрешность. Таким образом, и в данном случае решение задачи идентификации являться
некорректным.
3.3. Идентификации ИХ на базе прямого метода наименьших квадратов
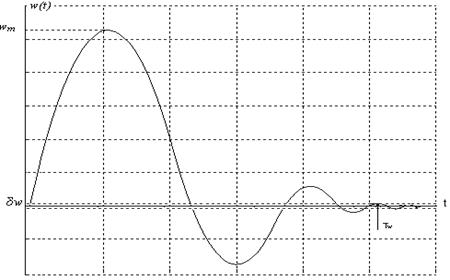
Рис. 3.1
На рис. 3.1
показана ИХ устойчивого объекта и ![]() при
при ![]() . На практике оперируют с, так называемой,
эффективной длительностью ИХ
. На практике оперируют с, так называемой,
эффективной длительностью ИХ ![]() , которая определяется
на уровне
, которая определяется
на уровне ![]() от максимального значения ИХ
от максимального значения ИХ ![]() .
.
Рассмотрим
уравнение (1.6) при ![]() и представим его в следующем виде
и представим его в следующем виде
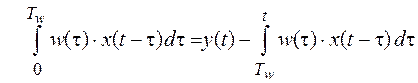 . (3.1)
. (3.1)
Обозначим
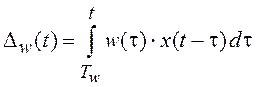 . (3.2)
. (3.2)
В
силу устойчивости объекта при ![]() слагаемое
слагаемое ![]() в выражении (3.1) принимает очень малые
(близкие к 0) значения.
в выражении (3.1) принимает очень малые
(близкие к 0) значения.
Запишем
(3.1) с учетом помех ![]() и
и ![]() ,
искажающих входной
,
искажающих входной ![]() и выходной
и выходной ![]() сигналы идентифицируемого объекта
сигналы идентифицируемого объекта
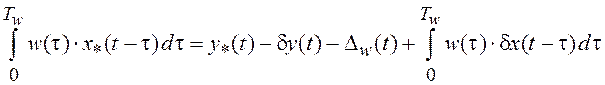 . (3.3)
. (3.3)
Далее,
переходя к дискретному времени ![]() ,
, ![]() ,
, ![]() получим
получим
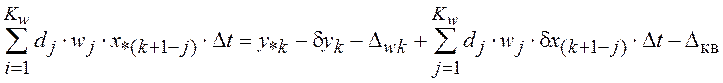 ,
, ![]() ,
,
или вводя нормированные отсчеты ИХ
![]() (3.4)
(3.4)
и обобщенную помеху
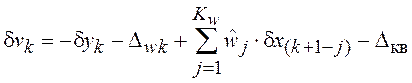 (3.5)
(3.5)
Окончательно будем иметь
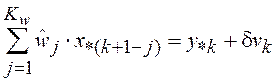 ,
, ![]() .
(3.6)
.
(3.6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.