Математические модели объектов управления. Общие сведения об идентификации. Идентификация импульсной и частотных характеристик. Структурная идентификация линейного стационарного объекта, страница 12

,    

и после несложных преобразований получим

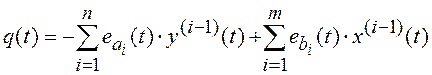.                       (7.6)

Теперь условие устойчивости (7.5) представим в виде

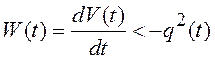.                                           (7.7)

Определим

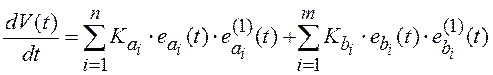                    (7.8)

и

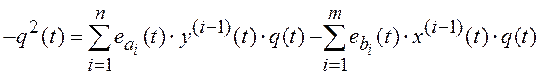.                (7.9)

Согласно (7.7) приравняем в левой и правой частях выражений (7.8) и (7.9) слагаемые при одинаковых ошибках  и . Получим

,         ,

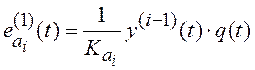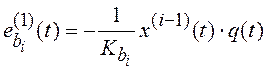,     , откуда, имея в виду, что 

   и    , а следовательно

,

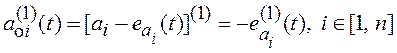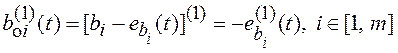
получим алгоритм идентификации

,   ,

,   .

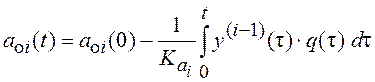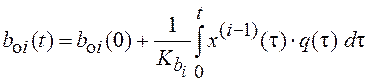Функцию  можно определить выражением

.

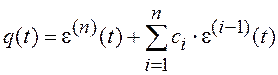Достоинством НГСМ является гарантия сходимости оценок ,  к параметрам ,  объекта при любых начальных условиях в отсутствии помех  и .

Недостатки.

1. НГСМ  описывается системой нелинейных, нестационарных, дифференциальных уравнений, заданных в неявной форме, поэтому оказывается невозможным провести теоретический анализ, точности и быстродействия алгоритма.

2. В алгоритм идентификации входят все производные входного и выходного сигналов объекта. Возникает необходимость их измерения.

3. Решение модельных задач иллюстрирует низкое быстродействие НГСМ, которое с увеличением n или  резко падает.

4. Отсутствует сглаживание высокочастотных составляющих помехи  из-за одинаковых порядков n левой и правой частей уравнения последовательной  модели.

8. ОЦЕНИВАНИЕ РАСШИРЕННОГО ВЕКТОРА СОСТОЯНИЯ

НЕЛИНЕЙНЫХ СТАЦИОНАРНЫХ ОБЪЕКТОВ

Пусть объект описывается нелинейной системой дифференциальных уравнений     

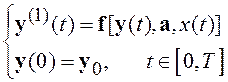,                                   (8.1)

где

.

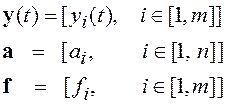Входной  и выходной  сигналы измеряются на интервале наблюдения . Для записи расширенного вектора состояния проделаем некоторые преобразования.

Переведем искомые параметры ,   в разряд переменных состояния объекта и дополним систему (1) новой системой дифференциальных уравнений, которая имеет вид

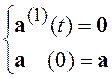.                                             (8.2)

Далее введем обозначения

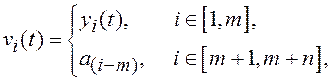
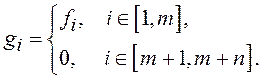
При этом

.

В результате система нелинейных дифференциальных уравнений относительно расширенного вектора состояния объекта , объединяющая системы (8.1) и (8.2), может быть представлена в виде

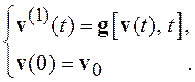                                           (8.3)

Решение системы (8.3) можно отыскать, например, методом квазилинеаризации  или инвариантного погружения. Рассмотрим первый из них.

В литературе известны 2 постановки задачи оценивания расширенного вектора состояния объекта:

1.  Наряду с искомыми параметрами  оценивается и переменные состояния

2.  Оценивается только параметры  а переменные состояния известны.

Для решения этих задач рекомендуют 2 метода: метод квазилинеаризации и метод инвариантного погружения.

Метод квазилинеаризации представляет собой итерационную процедуру, на каждом -ом шаге которой (), вычисляется  -ая оценка  вектора  посредством решения некоторой системы линейных алгебраических уравнений. Данная система получается при аппроксимации функции  рядом Тейлора в окрестности . Полагая  и учитывая только линейную часть ряда Тейлора, можно перейти от нелинейной дифференциальной системы (8.3) к линеаризованной системе алгебраических уравнений вида

             (8.4)

где

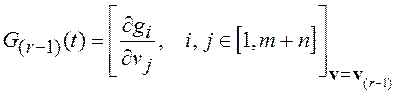.                     (8.5)

Формально решение системы (8.4) может быть представлено как

,                                   (8.6)

где матрица  является решением однородной матричной системы дифференциальных уравнений

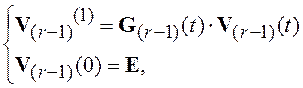                                 (8.7)

а вектор  представляет собой решение неоднородной дифференциальной

системы

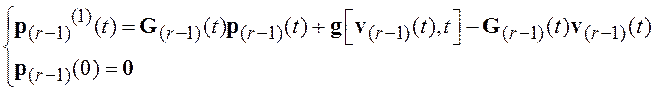 .      (8.8)

Предполагается, что метод квазилинеаризации сходится, т.е. имеет место

.

Тогда, при  будем иметь

,   , а при  ( - количество итераций)

.

Поэтапно метод квазилинеаризации выглядит следующим образом.

На основании некоторых физических соображений задается начальное условие -  оценка вектора , а далее организуется итерационная процедура, на каждом -ом, , шаге которой выполняются следующие операции:

1) формируется матрица  вида (8.5), элементы которой вычисляются как ,   путем решения уравнения чувствительности;

2) определяется матрица  посредством решения однородной дифференциальной системы (8.7), мерность которой ;