Исследование числовых матриц на линейную независимость строк. Элементарные операции. Гауссово исключение. Преобразование Хаусхольдера. Строчно поисковый алгоритм. Форма Гейзенберга, страница 3

и так далее. В матрице К₁ е_i1=-a_ik/a_1k,   Тогда к-й столбец матрицы , за исключением первого элемента, нулевой столбец. Здесь . Пусть  некоторый ненулевой элемент второй строки К₁А. Пусть К₂ будет вида ране указанного с . Тогда j столбец матрицы , где  за исключением первых двух элементов, содержит нулевые элементы. Если в результате этого процесса в некоторой строке не окажется нулевого элемента, то полагаем К_i равной единичной матрице, и переходим к следующей строке. Если проведем этот процесс до последней строки, то получим

≜                                                        (1.5)

где K≜ .Так как каждая К_i нижнетреугольная матрица с единицей на диагонали, то такой же вид у матрицы А. Если j-я строка  нулевой строчный вектор, тогда j-я строка А линейно зависит от предыдущих строк. Далее, коэффициенты соотношения

                                  (1.6)

с b_jj=1 есть в точности j-я строка К.

Матрица К может быть вычислена прямым перемножением К_i, , что сложно. Введем следующий рекурсивный способ перемножения строк К. Прежде всего мы запомним  i -й столбец K_i в i-м столбце матрицы

                                       (1.7)

Для вычисления j-й строки К возьмем первые j строк матрицы F затем перенесем j-ю строку К под нее

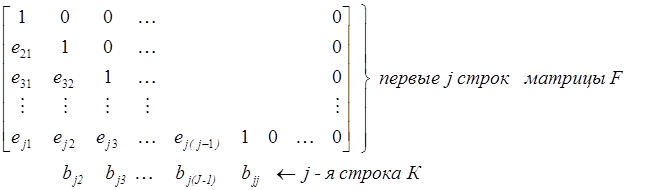(1.8)

Можно непосредственно проверить, что

                 (1.9)

Мы видим, что b_jk есть в точности скалярное  (внутреннее) произведение (inner product) вектора из матрицы на вектор под матрицей, как показано в (1.8). Таким образом коэффициенты соотношения (1.6) или эквивалентно, j- строка К может быть вычислена с использованием этой простой процедуры.

При работе с данным алгоритмом не нужна подробная информация о матрицах, входящих в произведение  . Нам нужны всего лишь несколько строк матрицы К. Таким образом, лучше запомнить К_i в F (1.7) и записывать (1.5) как

.                                (1.10)

Таким образом, если нам нужны строки  К, то мы будем использовать процедуру (1.8) и (1.10) для вычисления строк K  из F.

Пример 1.1. Найдем линейно зависимые строки 

2

.

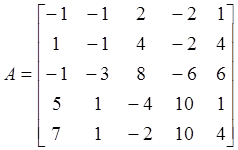Выберем элемент (1,3) в качестве ведущего и вычислим

2

3

≜ .

Первый столбец K₁-это третий столбец A деленный на –2. Далее мы выбираем  элемент (2,1) матрицы А₁ как ведущий и вычислим

	2

 

3

≜.

Так как третья строка А₂ нулевая, полагаем К₃ =I и переходим к следующей строке. Вычислим

2

4

3

≜.

Последняя строка  нулевая, и поиск закончен. Используя (1.10), можем записать

≜.

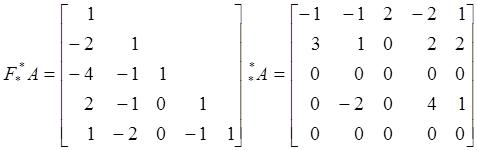Отметим ,что i- й столбец F есть i- столбец К_ii = 1,2,3,4. Так как третья строка  нулевая, то она линейно зависит от ее предыдущих двух строк. Аналогично, пятая строка А линейно зависит от ее предыдущих четырех строк.

Для определения коэффициентов соотношения для третьей строки А вычислим, используя (1.9), из первых трех строк F

.

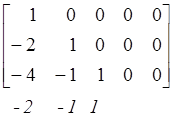Следовательно, имеем

или

                                                                                        (1.11)

где а_ii- строка А.

Для определения комбинации пяти строк А вычислим

Отсюда имеем

или

 .                                        (1.12)