Поисковые методы оптимизации составляют класс методов нелинейного программирования. Вспомним еще раз постановку задачи оптимизации:
![]() (3.1)
(3.1)
при условиях
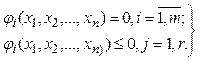 (3.2)
(3.2)
Часто критерий ![]() не
имеет явного выражения, либо функции(3.1), (3.1) являются трудно вычислимыми
нелинейными функциями. Задачи такого типа составляют предмет нелинейного
программирования.
не
имеет явного выражения, либо функции(3.1), (3.1) являются трудно вычислимыми
нелинейными функциями. Задачи такого типа составляют предмет нелинейного
программирования.
Как правило, решение задач нелинейного программирования
может быть найдено только численными методами. В настоящее время для решения
надобных задач разработано значительное число методов. Однако все еще не
предоставляется возможным отдать предпочтенное какому-либо одному из них.
Поисковые методы оптимизации основаны на постоянном перемещении в пространстве
переменных в направлении к оптимальному значению функции![]() .
Различные методы поиска отличаются способом определения направления движения к
оптимуму, размером шага и продолжительного поиска вдоль найденного направления,
критериями окончания поиска, простотой алгоритмизации для ЭВМ.
.
Различные методы поиска отличаются способом определения направления движения к
оптимуму, размером шага и продолжительного поиска вдоль найденного направления,
критериями окончания поиска, простотой алгоритмизации для ЭВМ.
Нормирование переменных. Переменные ![]() в конкретных
задачах могут иметь самый различный физический смысл и разные единицы
измерения. Поэтому при решении оптимальных задач численными методами
целесообразно оперировать с их безразмерными нормализованными значениями.
в конкретных
задачах могут иметь самый различный физический смысл и разные единицы
измерения. Поэтому при решении оптимальных задач численными методами
целесообразно оперировать с их безразмерными нормализованными значениями.
Обычно для нормализации применяется возможный диапазон изменения значений независимых переменных
![]() .
.
Вводя безразмерные переменные
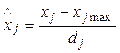 ;
; ![]() , (3.3)
, (3.3)
исходную
задачу (3.1), (3.2) выражают через них, решают преобразованную задачу,
определяют оптимальное значения нормированных переменных ![]() , а через них оптимальные значения
исходных переменных,
, а через них оптимальные значения
исходных переменных, ![]() :
:
![]() ;
;
при 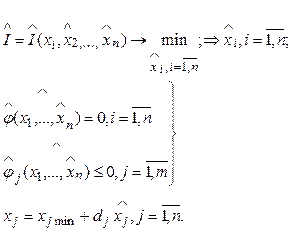
Линии уровня. В
соответствии с (3.1) критерий ![]() может рассматриваться
как функция, определенная n-мерном пространстве переменных
может рассматриваться
как функция, определенная n-мерном пространстве переменных ![]() Поскольку наглядное графическое
изображение n-мерного пространства отсутствует, обычно используется
прием представления
Поскольку наглядное графическое
изображение n-мерного пространства отсутствует, обычно используется
прием представления ![]() на плоском чертеже. Все
методы оптимизации сводятся к тому, чтобы найти минимум или максимум, т.е.
впадину или вершину на поверхности, описываемой уравнением
на плоском чертеже. Все
методы оптимизации сводятся к тому, чтобы найти минимум или максимум, т.е.
впадину или вершину на поверхности, описываемой уравнением ![]() . Эта поверхность называется поверхностью
отклика. Линии, вдоль которых целевая функция
. Эта поверхность называется поверхностью
отклика. Линии, вдоль которых целевая функция ![]() сохраняет
постоянное значение при изменении входящих в нее переменных, называются контурными
линиями или линиями уровня.
сохраняет
постоянное значение при изменении входящих в нее переменных, называются контурными
линиями или линиями уровня.
Примеры линией уровня показаны на рис.3.1 (при отсутствии ограничений), на рис.3.2 (при наличии ограничений) и на рис.3.3 (в окрестности седловой точки).

Рисунок 3.2 – Линии уровня без ограничений

Рисунок 3.3 – Линии уровня с ограничениями
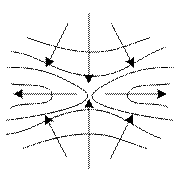
Рисунок 3.4 – Линии уровня в окрестностях седловой точки
Точки, в которых ![]() на
одним направлениям имеет минимум, а по другим – максимум, называются Седловыми
точками функции
на
одним направлениям имеет минимум, а по другим – максимум, называются Седловыми
точками функции ![]() . В этой точке хотя
выполняется необходимое условие
. В этой точке хотя
выполняется необходимое условие ![]()
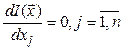 экстремума
функции
экстремума
функции ![]() в ней нет. Линии уровня,
соответствующие разным значениям
в ней нет. Линии уровня,
соответствующие разным значениям ![]() , не пересекаются.
Внутри линии уровня, соответствующие числам I, больше, чем I, в
случае максимума и меньше, чем I, в случае минимума.
, не пересекаются.
Внутри линии уровня, соответствующие числам I, больше, чем I, в
случае максимума и меньше, чем I, в случае минимума.
Поисковые методы оптимизации основаны на постоянном
перемещении в пространстве переменных в направление к оптимальному значению
функции ![]() .
.
Различные методы поиска отличаются способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, критерия окончания поиска, простой алгоритмизации для ЭВМ.
Вычисление производных и градиента. В основу градиентных методов поиска оптимума положены
вычисления и анализ производных 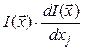 ,
, ![]() , вычисляются аналитически, если это
не представляет особого труда, либо численным методом по приближенному соотношению,
основанному на замене частных производных
, вычисляются аналитически, если это
не представляет особого труда, либо численным методом по приближенному соотношению,
основанному на замене частных производных ![]() в
точке
в
точке ![]() отношениями конечных приращений. Для
этого в точке
отношениями конечных приращений. Для
этого в точке ![]() поочерёдно изменяют
переменные
поочерёдно изменяют
переменные ![]() и вычисляют соответствующие приращения
в точке
и вычисляют соответствующие приращения
в точке ![]()
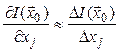 ,
, ![]() , (3.4)
, (3.4)
где ![]()
При применении нормализованных переменных ![]() в алгоритме оптимизации необходимо
учесть соотношение (3.3) при вычислении
в алгоритме оптимизации необходимо
учесть соотношение (3.3) при вычислении ![]() ,
если она выражена через значения исходных физических переменных
,
если она выражена через значения исходных физических переменных ![]() :
:
![]() .
(3.5)
.
(3.5)
Для вычисления производных ![]() удобно
давать одно и то же приращение
удобно
давать одно и то же приращение ![]() но всем
независимым переменным
но всем
независимым переменным ![]() , т.е.
, т.е.
![]() ,
, ![]()
тогда
![]() ,
, ![]()
Формула (3.4) дает лишь приближенное значение
производной 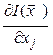 . Точность этого приближения зависит
от приращения независимой переменной
. Точность этого приближения зависит
от приращения независимой переменной ![]() . Априорных
способов предсказания наилучшего значения
. Априорных
способов предсказания наилучшего значения ![]() не
существуют. Можно лишь заметить, что допустимое приращение
не
существуют. Можно лишь заметить, что допустимое приращение ![]() по максимуму ограничено кривизной
целевой функции
по максимуму ограничено кривизной
целевой функции ![]() в исследуемой точке
(которая заранее не известна), а по минимуму- погрешностью вычисления значения
функции
в исследуемой точке
(которая заранее не известна), а по минимуму- погрешностью вычисления значения
функции ![]() (которая тоже заранее не известна и
может существенно отличаться от погрешности задания значений
(которая тоже заранее не известна и
может существенно отличаться от погрешности задания значений ![]() в процессе поиска).
в процессе поиска).
На практике для определения приемлемого значения ![]() (в особенности в начале поиска,
когда произведение еще ни разу не находилось) используют метод дробления
(в особенности в начале поиска,
когда произведение еще ни разу не находилось) используют метод дробления ![]() . Вычисляют значение производной
. Вычисляют значение производной 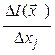 с приращением
с приращением ![]() . Расчет повторяют с
. Расчет повторяют с ![]() . Если полученные значения
производных различаются существенно, расчет повторяется с
. Если полученные значения
производных различаются существенно, расчет повторяется с ![]() и т.д., пока не будет найдено
приемлемое значение приращения
и т.д., пока не будет найдено
приемлемое значение приращения ![]() . На последующих
шагах это значение может уточняться.
. На последующих
шагах это значение может уточняться.
Градиент в точке ![]() равен
равен
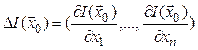 .
.
3.2 Градиентные методы оптимизации
3.2.1 Метод релаксации
Алгоритм метода заключается в отыскании осевого направления, вдоль которого целевая функция уменьшается наиболее сильно ( при поиске минимума). Рассмотрим задачу безусловной оптимизации
![]() (3.6)
(3.6)
Для определения осевого направления в начальной точке ![]() поиска из области
поиска из области ![]() определяются производные
определяются производные 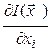 ,
, ![]() ,
по всем независимым переменным. Осевому направлению соответствует наибольшая по
модулю производная
,
по всем независимым переменным. Осевому направлению соответствует наибольшая по
модулю производная 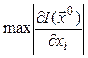 .
.
Пусть ![]() – осевое
направление, т.е.
– осевое
направление, т.е. 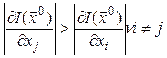 .
.
Если знак производной 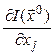 отрицательный,
функция
отрицательный,
функция ![]() убывает в направлении оси, если
положительный – в обратном направлении:
убывает в направлении оси, если
положительный – в обратном направлении:
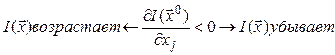
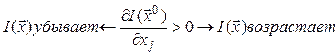
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.