Как видно, метод дихотомии позволяет довольно быстро попадать в район оптимума. Так, после 10 шагов дихотомии (20 измерений показателя качества) длина интервала неопределенности, где локализован оптимум, в 210=1024 раза меньше исходной длины l = b – a. Для достижения такой точности в методе равномерного приближения потребуется вычисление I(x) в 1025 точках.
1.5 Метод золотого сечения
В геометрии золотым сечением называется такое деление отрезка на две неравные части, при котором отношение всего отрезка к большей части равнялось отношению большей части к меньшей. Первым человеком, который делил линейный отрезок подобным образом, был Евклид. Благодаря многочисленным удивительным свойствам этого соотношения ученые эпохи Возрождения предавали ему почти мистическое значение. Кеплер, например, ставил его рядом с теоремой Пифагора. Освященное веками прославленное золотое сечение в настоящее время нашло эффективное применение в задачах оптимизации.
Метод, разработанный американскими специалистами Кифером и Джонсоном, применим для класса унимодальных функций.
Пусть максимум критерия I(x) находится в интервале [a, b] оси x (внутри или на его краях). По принципу золотого сечения количество пробных точек принимается равным двум, причем они должны размещаться на одинаковых расстояниях от середины интервала таким образом, чтобы отношение длины исключаемого подынтервала к величине интервала поиска оставалось постоянным. При этом на двух следующих друг за другом шагах всегда будет иметь место отношение
где lk – длина интервала неопределенности после k-го шага поиска.
Отсюда с учетом lk-1= lk + lk+1 находим
t2 + t – 1= 0.
Положительный корень этого уравнения (отрицательный не имеет смысла) равен
Таким образом, в соответствии с рассматриваемым методом пробные точки x1 и x2 на оси x располагаются следующим образом
x1 = a + (1 – t)´(b – a);
x2 = a + t ´(b – a).
В результате анализа двух значений I(x1) и I(x2) целевой функции I(x) исключатся один из подинтервалов, где оптимума заведомо быть не может, и выбирается новый интервал неопределенности, который должен исследоваться в дальнейшем. Этот интервал будет состоять из двух неравных отрезков, являющихся отрезками золотого сечения, и содержать одну из предыдущих точек. Симметрично ей выбирают вторую точку внутри нового интервала изложенным выше способом и вычисляют значение функции I(x) в новой точке. Путем анализа двух значений функции I(x) (одно из них получено в предыдущем шаге поиска) определяют новый интервал неопределенности и т. д.
Поиск оптимума завершается, если после k-го шага длина интервала неопределенности станет меньше или равна d, т. е. lk £ d, где d – заданная погрешность определения оптимума.
Такая стратегия поиска оптимума позволяет сужать интервал неопределенности, каждый раз вычисляя лишь одно значение I(x), а не два, как в методе дихотомии.
Длина интервала неопределенности после k испытаний критерия I(x) равна
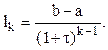
При k=20 (20 измерений показателя качества) 
, что почти в 10 раз меньше длины
интервала неопределенности при поиске максимума методом дихотомии.
1.6 Метод квадратичной интерполяции
Этот метод может непосредственно применяться к унимодальным функциям одной переменной. Он может быть очень полезным для поиска частного оптимума по отдельным направлениям при решении задач многомерной оптимизации.
В предыдущих двух методах была сделана попытка найти малый интервал, в котором находятся оптимум функции I(x). В рассматриваемом методе применяется иной подход. Он заключается в построении аппроксимирующей модели оптимизируемой функции I(x). Функция I(y) может быть аппроксимирована полиномом второго порядка
(1.5)
по крайней мере, в небольшой области значений, в том числе в области оптимума. При этом положение экстремума I(x) определяется положением экстремума полинома (1.5), поскольку последний вычислить проще.
Экстремум функции Ia(x), как известно, расположен в точке
(1.6)
Положим, что окрестность некоторой исходной точки x=x1 на области определения I(x) аппроксимирована полиномом (1.5). Задача поиска заключается в определении смещения
(1.7)
которое приводит из исходного состояния x=x1 в экстремальное x=x*. Если I(x) строго квадратичная функция, то смещение Dx после первого шага сразу приведет к x*. В противном случае достижение x* требует выполнения итерационной процедуры.
Для определения смещения Dx нужно определить коэффициенты параболы (4.5). Эта задача легко решается, если известны значения I(x) в трех точках. Пусть вычисление I(x) производилось в районе исходного состояния x=x1 в точках x1, x0=x1-h, x2=x1+h и при этом получено три значения этой функции:
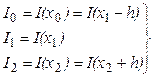(1.8)
где h – полуинтервал интерполяции, малая постоянная положительная величина.
Подставляя эти значения в уравнение (1.5), получаем систему из трех линейных уравнений с тремя неизвестными a, b и с:
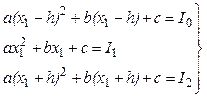(1.9)
Для того, чтобы эта система имела решение, необходимо, чтобы ее определитель не был равен нулю, то есть
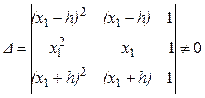(1.10)
Раскрывая этот определитель, находим
,
что всегда выполняется, поскольку h¹0.
Разрешая систему уравнений (1.9), получаем интересующие нас значения параметров a, b, c и, подставляя их в формулу (1.6), находим положение экстремума параболы
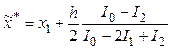(1.11)
Величина рабочего смещения Dx равна
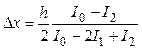(1.12)
Зная коэффициенты a, b, с можно определить и экстремальное значение функции (1.5) по формуле
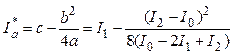(1.13)
которое является оценкой экстремума критерия I(x).
После выполнения рабочего шага Dx следует
проверить, действительно ли найден экстремум. Для этого достаточно вычислить
значение функции цели I(x) в предполагаемом экстремуме 
и
сопоставить его с оценкой (1.13). Если эти величины отличаются не более чем на e, то есть
(1.14)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.