Кинематическая схема механизма предназначена для определения положений, траекторий, скоростей и ускорений точек и звеньев механизма. Для построения кинематических схем используются условные обозначения согласно ГОСТ 2770 – 68.
Планы положений механизма строятся методом засечек в масштабе (рис.2). В отличие от масштабов, применяемых в машиностроении, в теории механизмов и машин масштабы представляют собой именованные числа. Масштабы обозначаются буквой К с соответствующим индексом:
Масштабы длин и пути 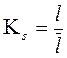 ,
м /мм;
,
м /мм;
Масштаб скоростей 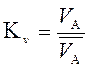 , м/с.мм;
, м/с.мм;
Масштаб ускорений ![]()
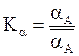 , м/с2.мм.
, м/с2.мм.![]()
Численное значение масштаба должно быть либо десятичной дробью, либо целым числом и включать в себя стандартные цифры или комбинации цифр: 1, 2, 4, 5, 15, 25, 75, 10, 20…….
Для выполнения кинематического анализа данного механизма в
задаче № 1 требуется вычертить в выбранном масштабе Кs
положение механизма изображенное в задании и для него построить план скоростей
и ускорений ![]()
Метод построения планов скоростей и ускорений основан на теореме о разложении движения, согласно которой любое движение можно представить как сумму двух простых движений – переносного /поступательного/ и относительного /вращательного/. Тогда для скоростей:
![]()
для ускорений:
![]() ,
,
где ![]() - нормальная составляющая ускорения
в относительном движении /определяется по данным плана скоростей/, на плане
ускорений всегда направлена вдоль звена к центру относительного движения;
- нормальная составляющая ускорения
в относительном движении /определяется по данным плана скоростей/, на плане
ускорений всегда направлена вдоль звена к центру относительного движения;
![]() - касательная составляющая
/определяется графически/ на плане ускорений, всегда направлена перпендикулярно
к звену /радиусу/ относительного движения.
- касательная составляющая
/определяется графически/ на плане ускорений, всегда направлена перпендикулярно
к звену /радиусу/ относительного движения.
Для определения скорости или ускорения точки графическим путем не-обходимо составить систему из двух векторных уравнений. При составлении векторных уравнений движение точки рассматривается относительно двух других точек, с которыми эта точка связана и скорости которых уже известны.
Пример:
Построить план скоростей и план ускорений для заданного положения механизма, изображенного на рисунке 2.
Пусть заданы размеры звеньев механизма: ОА = 150мм; АВ = 450мм и т.д. и частота вращения входного звена / кривошипа/ОА/, соответствующая n = 200 об/мин.
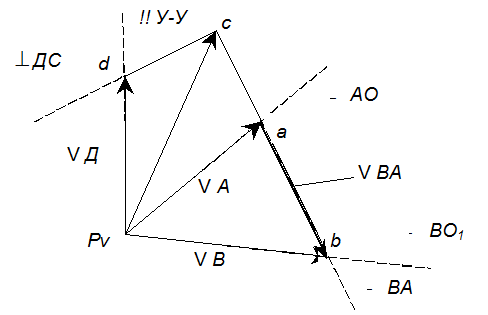
План скоростей рис.3.
Скорость пальца кривошипа /точка А/ определяется по формуле:
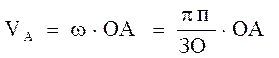 ,
,
где n - частота вращения кривошипа, об/мин;
ОА – длина кривошипа, м;
Подставляя данные в формулу, получим:
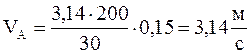
Задаваясь длиной отрезка ![]() /мм/, изображающего на плане скоростей
вектор скорости точки А, получим масштаб плана
/мм/, изображающего на плане скоростей
вектор скорости точки А, получим масштаб плана ![]() :
:
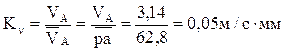
Отрезок ![]() :
:
![]() = 62,8 мм
= 62,8 мм
выбран так, чтобы был получен стандартный масштаб скоростей.
Рекомендуется выбирать отрезок ![]() не менее 50мм.
не менее 50мм.
Из полюса плата скоростей р отложим
вектор скорости точки А ![]() перпендикулярно
звену ОА/ по касательной к траектории движения точки А/ в сторону ее движения.
перпендикулярно
звену ОА/ по касательной к траектории движения точки А/ в сторону ее движения.
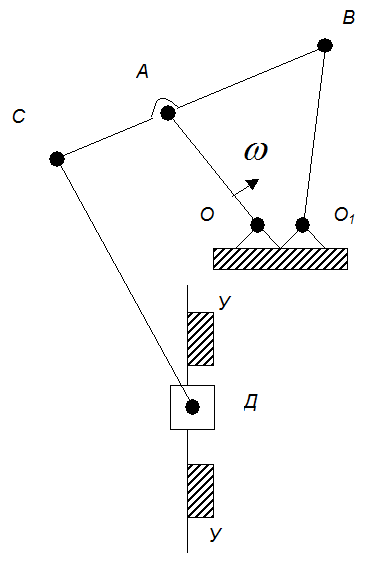
Рис.2. План механизма
КS=………………м/мм
.
КV…………………….м/с*мм
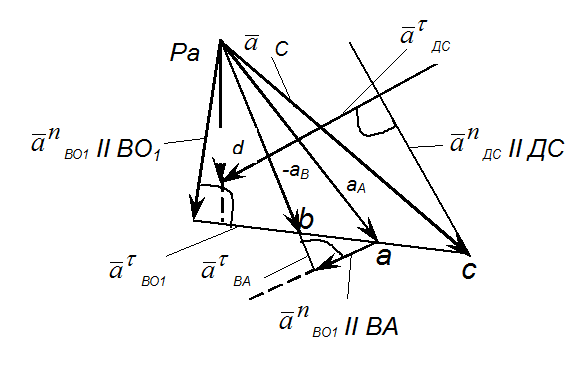 Рис.4. План ускорений
Рис.4. План ускорений
Кa……………………………м/с2мм
Рассматривая движение точки В относительно точки А, а затем относительно ОI, имеем:
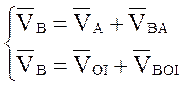
Из конца вектора скорости ![]() /точка
а/ проводим линию действия вектора относительной скорости
/точка
а/ проводим линию действия вектора относительной скорости ![]() перпендикулярно звену АВ, а затем из
полюса p /т.к. V0 =
0/ перпендикулярно звену ВОI проводим
линию действия вектора относительной скорости
перпендикулярно звену АВ, а затем из
полюса p /т.к. V0 =
0/ перпендикулярно звену ВОI проводим
линию действия вектора относительной скорости ![]() до
пересечения с линией действия вектора
до
пересечения с линией действия вектора ![]() в
точке в. Отрезок
в
точке в. Отрезок![]() изображает вектор
абсолютной скорости точки В
изображает вектор
абсолютной скорости точки В ![]() .
.
Скорость точки С /третьей точки звена ВАС/ найдем методом подобия. Можно записать следующее соотношение:
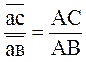 или
или 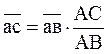 ,
,
где ![]() и
и ![]() - отрезки на плане скоростей;
- отрезки на плане скоростей;
АС и АВ – размеры звеньев механизма.
Вычислив отрезок ![]() и отложив его на
плане скоростей, получим точку
и отложив его на
плане скоростей, получим точку ![]() . Соединяя точку
. Соединяя точку ![]() с полюсом
с полюсом ![]() , найдем отрезок
, найдем отрезок ![]() , изображающий вектор абсолютной
скорости точки С (Vc).
, изображающий вектор абсолютной
скорости точки С (Vc).
Для определения скорости точки Д рассмотрим движение этой точки относительно точек С и Ду / точка Ду принадлежит неподвижным направляющим и в данный момент совпадает с точкой Д /.
Система векторных уравнений имеет вид:
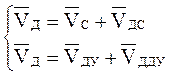
Так как VДУ =0, то ![]() .
.
Из конца вектора скорости ![]() точка
с / проводим линию действия вектора относительной скорости
точка
с / проводим линию действия вектора относительной скорости ![]() перпендикулярно звену СД,
а из полюса p параллельно оси у-у проводим линию
действия вектора относительной скорости
перпендикулярно звену СД,
а из полюса p параллельно оси у-у проводим линию
действия вектора относительной скорости ![]() в
точке d . Отрезок
в
точке d . Отрезок ![]() изображает вектор абсолютной
скорости точки Д
изображает вектор абсолютной
скорости точки Д ![]() .
.
Абсолютные скорости каждой точки равны:
VВ = ![]() , м/с
, м/с
VС = ![]() , м/с
, м/с
VД = ![]() , м/с
, м/с
Относительные скорости:
VВА = ![]()
![]() =
= ![]()
VДС = ![]()
План ускорений рис.4.
Рассматривая движение точки А относительно точки О, можно записать:
![]()
Ускорение ао = 0, 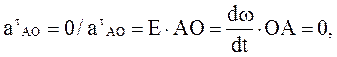 т.к.
т.к.
![]() сonst. Следовательно, точка А при
постоянной угловой скорости кривошипа будет иметь только нормальное /
центральное/ ускорение:
сonst. Следовательно, точка А при
постоянной угловой скорости кривошипа будет иметь только нормальное /
центральное/ ускорение:
![]()
Величина нормального ускорения: 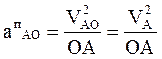
Подставляя числовые значения, получим:
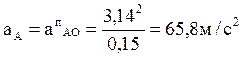
Задаваясь длиной отрезка ![]() изображаемого
на плане ускорений вектор ускорения точки А, получим масштаб плана ускорений
изображаемого
на плане ускорений вектор ускорения точки А, получим масштаб плана ускорений ![]()
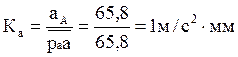
Отрезок ![]() выбран равным 65,8 мм, чтобы получить стандартный масштаб ускорений.
выбран равным 65,8 мм, чтобы получить стандартный масштаб ускорений.
Из полюса плана ускорений ![]() откладываем
вектор ускорения точки А
откладываем
вектор ускорения точки А ![]()
/отрезок ![]() /
параллельно звену АО, направляя его от точки А к центру ее вращения – точке О.
/
параллельно звену АО, направляя его от точки А к центру ее вращения – точке О.
Рассматривая движение точки В относительно точки А, а затем относительно точки О1, имеем:
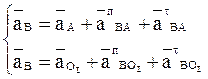
Так как ![]() то
то ![]() .
.
Нормальное ускорение В в ее относительном движении относительно точки А по величине определяется следующим образом:
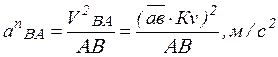
Удобнее сразу находить величину отрезка, изображаемого вектор нормального ускорения:
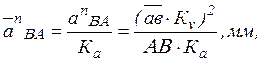
где ![]() -
отрезок, изображений вектор относительной скорости
-
отрезок, изображений вектор относительной скорости ![]() на
плане скоростей, мм;
на
плане скоростей, мм;
АВ – длина шатуна, м.
Направлен вектор ![]() по шатуну от точки
В к точке А.
по шатуну от точки
В к точке А.
Вектор касательного ускорения ![]() известен
только по направлению – линия его действия перпендикулярна звену ВА.
известен
только по направлению – линия его действия перпендикулярна звену ВА.
Нормальное ускорение:
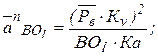
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.