где ![]() - собственные числа матрицы D.
- собственные числа матрицы D.
Норма (2.5.6) называется --Евклидова норма
Две нормы в конечномерном пространстве эквивалентны между собой вследствии выполнения цепочки неравенств
![]() . (2.5.6)
. (2.5.6)
2.6 Подобие матриц.
Две матрицы, соответствующие одному и тому же преобразованию в различных базисах, называются подобными.
Пусть y = A ∙ x и η = B ∙ ξ, тогда матрица A реализует линейное преобразование в некотором базисе и матрица B линейное реализует преобразование в другом базисе.
Если существует S – матрица перехода от первого базиса ко второму, то x = S ∙ ξ y = S ∙ η или y = S ∙ η = A ∙ S ∙ ξ = S ∙ η или S ∙ A ∙ S ∙ ξ = η или B = S -1 ∙ A ∙ S.
Итак, матрицы подобны, если существует ∙такая матрица S, что
det S ≠ 0 и B = S -1 ∙ A ∙ S (2.6.1)
Свойства:
а) det B = det A;
б) B и A имеют одинаковые характеристические полиномы и следовательно одинаковые собственные числа (включая их кратность).
2.7 Матрицы специальных видов.
Матрица Q называется ортогональной, если
QТ ∙ Q = Е или QТ = Q-1 (2.7.1)
Свойства:
а) в случае квадратных матриц Qортогональна тогда и только тогда, когда сумма квадратов элементов каждой ее строки равна 1, а сумма произведений соответствующих элементов любых различных строк равна 0 (аналогично для столбцов).
б) det Q = ± 1.
Доказательство: Q ∙ Q -1 = E , следовательно det Q ∙ det Q Т = (det Q)2 = 1 а значит det Q = ± 1.
Ортогональные матрицы
задают переход от одного ортонормированного базиса в пространстве к другому
ортонормированному базису. Причем это линейное преобразование ![]() сохраняет скалярный квадрат
вектора (аφ; аφ) = (а; а).
сохраняет скалярный квадрат
вектора (аφ; аφ) = (а; а).
Матрица называется идемпотентной (матрицей идемпотентного преобразования), если
Р2 = Р. (2.7.2)
Матрица называется инволютной, если
I 2 = E. (2.7.3)
3. ТОЧНЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Методы решения алгебраических задач подразделяют на точные, итерационные и вероятностные с малым, средним и большим числом неизвестных соответственно.
Приведенные в этом разделе методы относятся к классу точных (т.е. в предположении отсутствия округлений они дают точное решение задачи после конечного числа арифметических и логических операций).
3.1 Метод Крамера
Система линейных уравнений в матричном виде А ∙ Х = В. Решение ищется по формулам Крамера
![]() =
= ![]() i=1…n(3.1.1)
i=1…n(3.1.1)
где ![]() получается из матрицы А
заменой в ней столбца с номером i на вектор-столбец В.
получается из матрицы А
заменой в ней столбца с номером i на вектор-столбец В.
Метод применим только для систем, у которых det A=Δ ≠ 0 и имеет единственное решение.
3.2 Матричный метод
![]() (3.2.1)
(3.2.1)
где ![]() находится по формулам (2.3.2).
находится по формулам (2.3.2).
Метод применим только для систем, у которых det A=Δ ≠ 0 и имеет единственное решение.
3.3 Метод Гаусса
Метод Гаусса – это метод последовательного исключения неизвестных.
а) Если а11 ≠ 0, то первую строку делим на а11, если а11=0 меняем строки местами.
б) от остальных строк
отнимаем 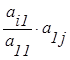 . Получаем новую матрицу, у которой
. Получаем новую матрицу, у которой
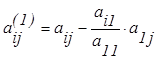 и
и ![]() =0
=0 ![]() (3.3.1)
(3.3.1)
и т.д. до получения треугольной матрицы.
Обратный ход метода Гаусса
в) 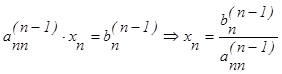 ;
(3.3.2)
;
(3.3.2)
и т.д. поднимаемся по рекуррентным формулам, получаем хn-1, … , x1.
3.4 Метод главных элементов
Метод главных элементов позволяет избежать влияния вычислительной погрешности. Метод состоит в следующем. В расширенной матрице системы выберем ненулевой, не принадлежащий В элемент аik, как правило наибольший по модулю.
![]()
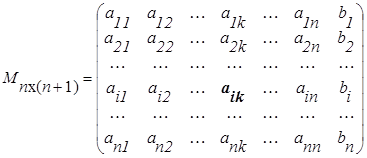 .
.
аik – называется главным элементом, строку с номером i – главной строкой.
Главную строку делим на аik, а затем от всех остальных строк отнимаем главную
строку, умноженную на ![]() . Таким образом, получаем рекуррентное соотношение:
. Таким образом, получаем рекуррентное соотношение:
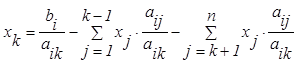 (3.4.1)
(3.4.1)
и матрицу ![]() , получаемую
вычеркиванием из исходной матрицы i- той строки и k-
того столбца. Так повторяем п раз. Метод главных элементов применяем
всегда, когда det A ≠ 0.
, получаемую
вычеркиванием из исходной матрицы i- той строки и k-
того столбца. Так повторяем п раз. Метод главных элементов применяем
всегда, когда det A ≠ 0.
Метод Гаусса является частным случаем метода главных элементов.
3.5 Схема Халецкого
Матрицу системы А представляют в виде произведения двух треугольных матриц А = В ∙ С
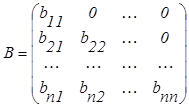 и
и 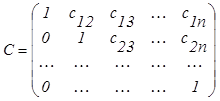 (3.5.1)
(3.5.1)
где элементы матриц В и С рассчитывают по формулам:
![]()
![]()
![]()
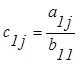
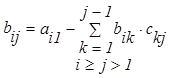
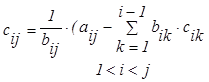 (3.5.2)
(3.5.2)
3.6 Решение линейных уравнений в среде "MathCad".
Линейные уравнения могут быть решены:
а) в матричном виде (размерность системы не выше 10×10);
б) при помощи функции LSOLVE (A,∙b) (категория функций "Решение"), аргументами которой являются А – матрица системы и b – столбец свободных членов;
в) при помощи функции rref (A) (категория функций "Вектор и Матрица"), где А – расширенная матрица системы (с действительными коэффициентами). Функция сводит матрицу системы к единичному виду, и в последнем столбце получаем ответ. Также при помощи этой функции можно исследовать систему на совместность.
4 ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Вообще-то говоря, для любой системы с невырожденной матрицей, существуют итерационные методы решения. Если метод итераций сходится, то он дает следующие преимущества перед методами, изложенными выше:
а) если итерации сходятся достаточно быстро, т.е. если для решения системы необходимо менее п итераций, то получаем выигрыш во времени так как при решении системы методом итераций необходимо произвести » п2 действий, а для метода Гаусса » п3;
б) погрешности округления в методе итераций оказываются значительно меньшими, чем в методе Гаусса. Тем более, что метод итераций является "само исправляющимся" методом, т.е. любая допущенная в вычислениях ошибка не влияет на конечный результат, т.к. ошибочное приближение можно рассматривать, как новый начальный вектор;
в) особенно выгоден метод при решении систем, у которых значительное число переменных равно нулю;
г) процесс итерации состоит в выполнении однообразных операций.
4.1 Метод простой итерации (метод Якоби).
Исходную систему
уравнений ![]() всегда можно преобразовать к виду:
всегда можно преобразовать к виду:
![]() , (4.1.1)
, (4.1.1)
так как ![]() , если D ≠ 0.
, если D ≠ 0.
И тогда ее решение сводится к нахождению предела последовательности
![]() (4.1.2)
(4.1.2)
Итерационный процесс называется сходящимся, если
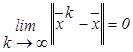 . (4.1.3)
. (4.1.3)
А уже из сходимости по норме следует покоординатная сходимость последовательных приближений.
Теорема (Достаточное условие сходимости – метода простой итерации).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.