Производная и ее приложения. Учебно-методическое пособие

проверки полученных знаний даны самостоятельные и контрольная работы.

Предназначено для студентов всех специальностей и составлено в соответствии с действующей программой по высшей математике.

УДК 517. 33(075.8)

                                                                       ББК 22.161.1

ISBN978-985-468-768-1Ó Щербо  А.  М.,  Шабалина  И.  П., Прокопенко А. И., 2010

Ó Оформление. УО «БелГУТ», 2010

1 ПРОИЗВОДНЫЕ ПРОСТЫХ ФУНКЦИЙ

Производной функции  в точке  называется предел отношения приращения функции к вызвавшему его приращению независимого переменного при условии, что это последнее стремится к нулю произвольным образом:

                               (1.1)

Нахождение производной  называют дифференцированием функции. Производная  представляет собой скорость изменения функции в точке .

Пример 1.1. Пользуясь определением производной, найти производную функции .

Решение. Найдем приращение функции

Тогда

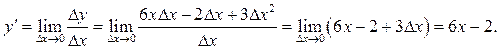
Имеют место следующие основные правила дифференцирования (здесь  – постоянная, а  и  – функции от , имеющие производные):

	(1.2)		(1.5)
	(1.3)		(1.6)
	(1.4)		(1.7)

Пользуясь приведенным определением производной, можно получить таблицу формул дифференцирования основных функций:

Пример 1.2. Найти производную функции

Решение. Основываясь на формуле (1.5), получаем

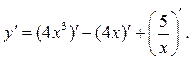
Далее, применяя формулу (1.4), имеем

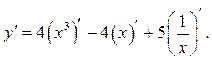
Применяя формулы (1.8), (1.3) и (1.5), получаем

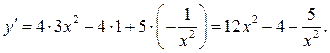
Естественно, при некотором навыке подобные промежуточные выкладки опускают.

Пример 1.3. Найти  если

Решение. Применяя формулы (1.7), (1.8) и (1.18), получим

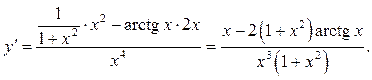
Если это целесообразно, т. е. ведет к упрощению дифференцирования, то функцию можно предварительно тождественно преобразовать, а потом уже находить производную.

Пример 1.4. Найти  если

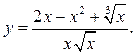
Решение. Преобразуем данную функцию:

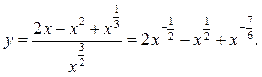
Тогда

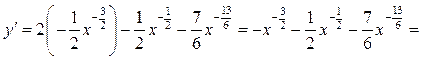
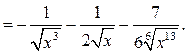
Задачи для самостоятельной работы

Используя правила дифференцирования и таблицу производных основных функций, найти производные:

1.1		1.2
1.3		1.4
1.5		1.6
1.7		1.8
1.9		1.10
1.11		1.12
1.13		1.14
1.15		1.16
1.17		1.18
1.19		1.20
1.21		1.22
1.23		1.24
1.25		1.26
1.27		1.28
1.29		1.30
1.31		1.32
1.33		1.34
1.35		1.36
1.37		1.38
1.39		1.40
1.41		1.42
1.43		1.44
1.45		1.46
1.47		1.48
1.49		1.50

2 ПРОИЗВОДНЫЕ СЛОЖНЫХ ФУНКЦИЙ

Пусть  и  – дифференцируемые функции. Тогда сложная функция  есть также дифференцируемая функция, причем

                                                

или

                                      

Это правило распространяется на цепочку из любого конечного числа дифференцируемых функций.

Пользуясь правилом дифференцирования сложной функции, можно получить таблицу более общих формул дифференцирования основных элементарных функций, где :

	(2.2)				(2.12)
	(2.3)				(2.13)
		(2.4)				(2.14)
		(2.5)				(2.15)
		(2.6)				(2.16)
		(2.7)				(2.17)
		(2.8)				(2.18)
		(2.9)				(2.19)
		(2.10)				(2.20)
		(2.11)				(2.21)

Пример 2.1. Найти  если

Решение. Полагая , где , согласно (2.2) будем иметь

Пример 2.2. Найти  если

Решение. Полагая , где , , находим

При дифференцировании сложных функций обычно обходятся без введения промежуточных аргументов  их только подразумевают. Например, последовательность нахождения производной функции, рассмотренной в данном примере, можно записать так:

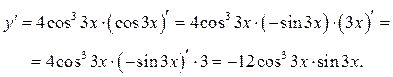
Кроме того, нет необходимости последовательно записывать, что сначала взята производная степенной функции с основанием , а затем производная косинуса и на последнем этапе производная его аргумента. Результат можно записать сразу:

В последующих примерах так и будем поступать.

Последовательность нахождения сложной производной можно задавать с помощью скобок. Для функции данного примера

Чтобы не путаться в сложных случаях при дифференцировании, можно рекомендовать придерживаться следующего правила: если подлежащая дифференцированию функция является результатом целого ряда действий над аргументом , то за промежуточный аргумент  следует принять результат всех этих действий, кроме последнего. Например, если , то , так как при вычислении последним действием является возведение в четвертую степень. Тогда производная

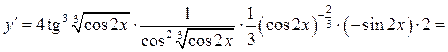
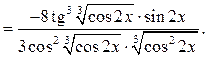
Пример 2.3. Найти производную функции

Решение.

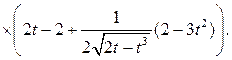
Пример 2.4. Найти производную функции

Решение.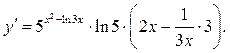

Пример 2.5. Найти производную функции

Решение.

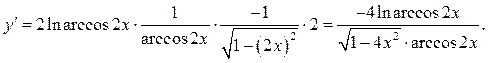
Пример 2.6. Найти производную

Решение.

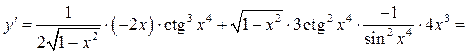
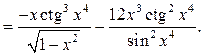
Пример 2.7. Вычислить , если

Решение. Находим производную заданной функции:

Подставляем в выражение производной вместо  единицу:

Задачи для самостоятельной работы

Найти производную функций:

2.1		2.2
2.3		2.4
2.5		2.6
2.7		2.8
2.9		2.10
2.11		2.12
2.13		2.14
2.15		2.16
2.17		2.18
2.19		2.20
2.21		2.22
2.23		2.24
2.25		2.26
2.27		2.28
2.29		2.30
2.31		2.32
2.33		2.34
2.35		2.36
2.37		2.38
2.39		2.40
2.41		2.42
2.43		2.44
2.45		2.46
2.47		2.48

3 ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ

ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ

Производная функции  при значении аргумента  равна угловому коэффициенту касательной, проведенной к графику этой функции в точке с абсциссой :

                                 (3.1)

Уравнение касательной к графику функции  в точке  имеет вид

                        (3.2)

Уравнение нормали, т. е. прямой, проходящей через точку касания , перпендикулярной касательной, записывается в виде

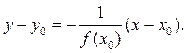                                        (3.3)

Производная функции , вычисленная при , т. е. , представляет собой скорость изменения функции относительно независимой переменной  в точке . Если зависимость между пройденным путем  и временем  при прямолинейном движении выражается формулой , то скорость  в любой момент времени  есть производная

                                      (3.4)

а ускорение (т. е. скорость изменения скорости движения)

                                                        (3.5)

Пример 3.1. Найти уравнение касательной и нормали к кривой  в точке

Решение. Находим производную и ее значение при :  

Воспользовавшись формулами (3.2) и (3.3), составим уравнение касательной:  и уравнение нормали:

Пример 3.2. Составить уравнение касательной к параболе  параллельной прямой

Решение. Чтобы составить уравнение касательной, нужно найти координаты точки касания . Для этого найдем угловой коэффициент прямой k_пр = 7 и на основании условия параллельности k_пр = k_кас получим k_кас Тогда

Уравнение касательной будет иметь вид

Пример 3.3. Тело движется прямолинейно по закону  ( выражается в метрах,  – в секундах). Найти скорость и ускорение движения через 1 с после начала движения.

Решение. Скорость прямолинейного движения равна производной пути по времени:

Тогда  (м/с).

Ускорение прямолинейного движения равно производной скорости по времени:  и, следовательно,  (м/с²).

Пример 3.4. Вращающееся колесо вагона задерживается тормозом. Угол , на который колесо поворачивается в течение  с, определяется равенством  Найти угловую скорость и угловое ускорение движения через 0,1 с после включения тормоза. Определить, в какой момент времени колесо остановится.

Решение. Угловая скорость движения колеса

Угловое ускорение

 т. е. ускорение постоянное.

Колесо остановится, когда скорость

Пример 3.5. Радиус основания цилиндра увеличивается со скоростью 3 м/с, а высота его уменьшается со скоростью 2 м/с. Какова скорость изменения объема цилиндра?

Решение. Объем цилиндра  где  – радиус основания,  – высота цилиндра. Продифференцируем обе части этого равенства по времени , учитывая, что  и  зависят от :

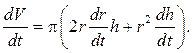
По условию  м/с,  м/с.

Тогда скорость изменения объема цилиндра

Пример 3.6. На кривой  найти точку, в которой ордината возрастает в два раза быстрее, чем абсцисса.

Решение. Находим производную

Так как производная характеризует скорость возрастания ординаты функции по сравнению с возрастанием абсциссы, то определим абсциссу точки из условия   а ордината точки  Получили точку

Пример 3.7. Под каким углом пересекаются линии  и

Решение. Под углом между двумя пересекающимися кривыми понимают угол между касательными к этим кривым, проведенным в точке их пересечения.

Найдем точку пересечения кривых, для чего совместно решим