Все радости жизни – в творчестве.
Творить – это значит убивать смерть.
Виктор Гюго
 глава
9
глава
9
ВОЗДЕЙСТВИЕ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ НА БЕЗЫНЕРЦИОННЫЕ НЕЛИНЕЙНЫЕ ЦЕПИ
9.1. Изучаемые вопросы
Одномерные законы распределения вероятностей случайного процесса на выходе безынерционного НЭ. Моменты (числовые характеристики). Действие стационарного случайного процесса (СП) на нелинейный преобразователь, односторонний и двухсторонний ограничитель, компаратор (пороговое устройство), квантователь, односторонний и двусторонний квадратор (квадратичный детектор) [3, 20.1¼20.4; 1, 11.1¼11.3; 2, 11.6].
Указания. Наиболее полно вопросы темы изложены в [3]. Руководства и учебные пособия [8, 9, 7, 5] содержат задачи с решениями, указаниями или комментариями.
Большинство практических задач можно подразделить
на два класса. Первый – это задачи по определению плотности вероятности
мгновенных значений выходного стационарного случайного процесса и/или первых
моментов распределения: математического ожидания, усредненного квадрата
(средней мощности на ![]() Ом) и дисперсии. Именно задачи
этого класса рассматриваются ниже.
Ом) и дисперсии. Именно задачи
этого класса рассматриваются ниже.
Ко второму классу относятся задачи, связанные с определением динамических характеристик выходного процесса: автокорреляционной функции и спектральной плотности мощности. Задачи этого класса, решаемые для нелинейных цепей, намного сложнее, чем для линейных, в большом количестве приведены в работах [8, 9], причем с решениями или указаниями к решению.
9.2. Краткие теоретические сведения
Плотность вероятности
На вход безынерционного НЭ, описываемого характеристикой ![]() , воздействует стационарный случайный
процесс
, воздействует стационарный случайный
процесс ![]() . По известной плотности вероятности
. По известной плотности вероятности ![]() входного процесса
входного процесса ![]() требуется
определить плотность вероятности
требуется
определить плотность вероятности ![]() выходного процесса
выходного процесса ![]() .
.
Если зависимость ![]() однозначна то вероятность
того, что случайная величина
однозначна то вероятность
того, что случайная величина ![]() заключена в интервале
заключена в интервале ![]() , должна быть равна вероятности пребывания
случайной величины
, должна быть равна вероятности пребывания
случайной величины ![]() в соответствующем интервале
в соответствующем интервале ![]() (рис. 9.1), т. е.
(рис. 9.1), т. е.
![]() (9.1)
(9.1)
или
![]() .
(9.2)
.
(9.2)
Из (9.2) следует, что
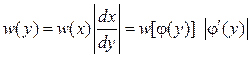 ,
(9.3)
,
(9.3)
где ![]() – функция, обратная
аппроксимирующей функции
– функция, обратная
аппроксимирующей функции ![]() ,
, ![]() . При этом производная берется по абсолютному
значению (модулю), так как функция
. При этом производная берется по абсолютному
значению (модулю), так как функция ![]() может быть
отрицательной, а плотность вероятности отрицательной быть не может.
может быть
отрицательной, а плотность вероятности отрицательной быть не может.
Если обратная функция ![]() в явном виде не выражается
или выражение весьма громоздкое (например, при аппроксимации
в явном виде не выражается
или выражение весьма громоздкое (например, при аппроксимации ![]() степенным полиномом), а по условию задачи
требуется изобразить
степенным полиномом), а по условию задачи
требуется изобразить ![]() , то поступают следующим образом.
Из выражения (9.1) находится плотность вероятности
, то поступают следующим образом.
Из выражения (9.1) находится плотность вероятности
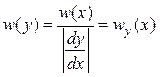 ,
(9.4)
,
(9.4)
которая зависит в явном виде от аргумента ![]() .
Задаются значения
.
Задаются значения ![]() , т. е.
, т. е. ![]() и
по известной зависимости
и
по известной зависимости ![]() и найденной зависимости
и найденной зависимости
![]() определяются соответствующие значения
определяются соответствующие значения ![]() . Полученные таким образом значения
. Полученные таким образом значения ![]() откладываются в координатах
откладываются в координатах ![]() . При необходимости эту графическую
зависимость можно аппроксимировать.
. При необходимости эту графическую
зависимость можно аппроксимировать.
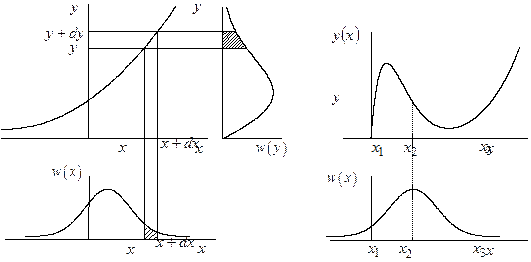
Рис. 9.1 Рис. 9.2
Если зависимость ![]() и, следовательно,
обратная зависимость
и, следовательно,
обратная зависимость ![]() неоднозначна (см.
рис. 9.2), то
неоднозначна (см.
рис. 9.2), то
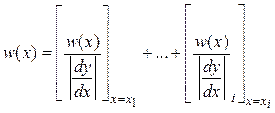 ,
(9.5)
,
(9.5)
где ![]() –
значения входной величины
–
значения входной величины ![]() , соответствующие
рассматриваемому значению
, соответствующие
рассматриваемому значению ![]() .
.
Если зависимость ![]() на
некотором расстоянии постоянна, то в выражение вида (9.3) – (9.5) должно
быть введено слагаемое с дельта-функцией. Это слагаемое должно учитывать вероятность
пребывания входной случайной величины
на
некотором расстоянии постоянна, то в выражение вида (9.3) – (9.5) должно
быть введено слагаемое с дельта-функцией. Это слагаемое должно учитывать вероятность
пребывания входной случайной величины ![]() ниже
(выше) определенного порогового значения
ниже
(выше) определенного порогового значения ![]() , до
которого (или с которого) зависимость
, до
которого (или с которого) зависимость ![]() постоянна.
постоянна.
На рис. 9.3, а, б показано воздействие стационарного случайного процесса на двусторонний ограничитель. Характеристика ограничителя описывается
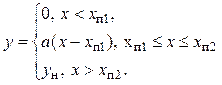 (линия 1 на
рис. 9.3, а).
(линия 1 на
рис. 9.3, а).
Плотность вероятности выходного процесса определяется по формуле (9.3) с добавлением двух дельта-функций
![]() , (9.6)
, (9.6)
учитывающих соответственно вероятности пребывания ![]() ниже порога
ниже порога ![]() и выше
порога
и выше
порога ![]() , т. е.
, т. е.
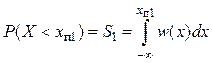 ,
, 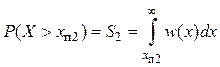 .
.
Значения коэффициентов ![]() и
и ![]() при дельта-функциях
при дельта-функциях ![]() и
и ![]() зависят
как от параметров сигнала – смещения
зависят
как от параметров сигнала – смещения ![]() и дисперсии
и дисперсии ![]() , так и от крутизны характеристики
, так и от крутизны характеристики ![]() НЭ.
НЭ.
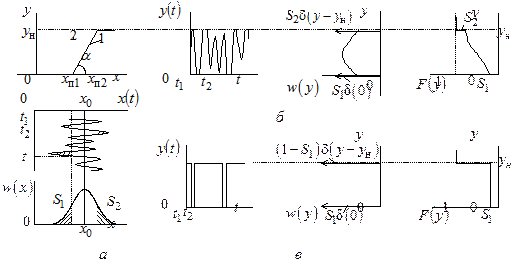
Рис. 9.3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.