Передаточная функция замкнутой системы. Передаточная функция ошибки от регулирующего воздействия, страница 2

Взяв только положительные значения частот, получаем:

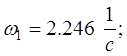
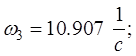                                                                                      (6.4)

Находим частоты пересечения вещественной оси:

                                           (6.5)

Откуда

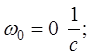
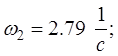                                                                                           (6.6)

Расположим все четыре частоты пересечения осей по порядку их возрастания и подчеркнем корни одного уравнения сплошной чертой, а другого – двойной:

Корни чередуются. Правило чередующихся корней выполняется, значит, система устойчива.

7. Годограф Михайлова.

Рис. 7.1. Годограф Михайлова.

Критерий устойчивости Михайлова:

Замкнутая система будет устойчива, если годограф характеристической частотной функции , начинаясь на вещественной оси, при изменении частоты от 0 до  последовательно против часовой стрелки обходит n квадрантов и заканчивается в n-ом  квадранте в бесконечности (число n определяется порядком системы).

Заданная система имеет 4 порядок, то есть годограф Михайлова должен последовательно обходить 4 квадранта комплексной плоскости и заканчиваться в бесконечности в 4-ом квадранте, что подтверждается рис. 7.1. Таким образом, заданная система является устойчивой.

   8. Исследование устойчивости системы по критерию Найквиста.

Критерий устойчивости Найквиста:

Для устойчивости замкнутой автоматической системы, устойчивой в разомкнутом состоянии, необходимо и достаточно, чтобы АФХ разомкнутого контура этой системы , построенная при изменении частоты  от  до , не охватывала критическую точку с координатами .

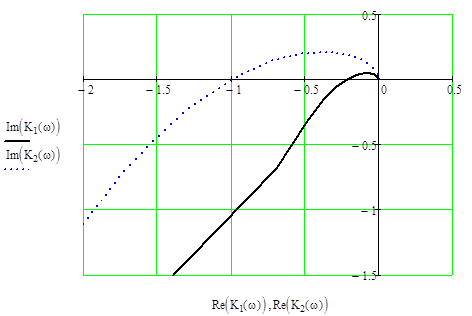
Как видно из рис. 9.1. пункта 9, годограф Найквиста, построенный для заданной системы при коэффициенте усиления системы , не охватывает точку с координатами , что означает устойчивость данной системы. На этом же рисунке приведен годограф, построенный для исследуемой системы при коэффициенте усиления . Как видно из рисунка, данный годограф пересекает вещественную ось в точке -1, при этом в системе наблюдаются незатухающие колебания.

      9. Годограф Найквиста.

                                                              Рис. 9.1. Годограф Найквиста.

На рис. 8.1 сплошной линией обозначен годограф Найквиста для системы с , пунктирной с .

10. Запас устойчивости по модулю и по фазе.

При изменении добротности условно устойчивой системы АФХ приближается к критической точке .  При этом переходная характеристика системы становится более колебательной – возрастает перерегулирование, длительность переходного процесса и число колебаний в переходном процессе. Чтобы указанные показатели качества переходного процесса не превышали допустимых по техническому заданию на проектируемую систему значений, АФХ должна быть несколько удалена от критической точки  .  Степень удаленности АФХ системы от критической точки характеризуется запасами устойчивости.

Запасом устойчивости по модулю  называют расстояние между критической точкой  и ближайшей к ней точкой пересечения АФХ с отрицательной полуосью абсцисс.

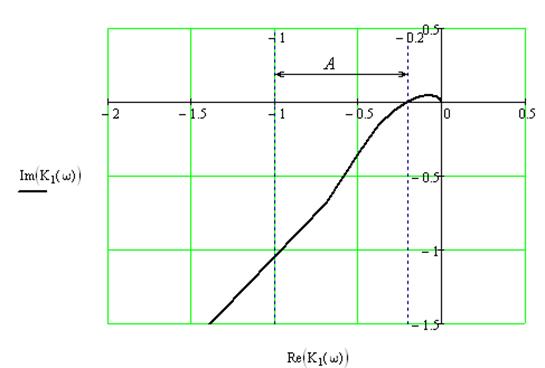
                      Рис. 10.1. Годограф Найквиста с указанием запаса устойчивости по модулю.