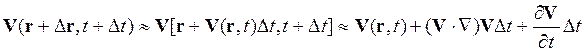Уравнения динамики атмосферы. Силы инерции. Уравнение неразрывности. Силы, действующие в атмосфере, страница 4

,

откуда для ускорения окончательно получаем

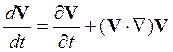
в полном соответствии с правилом (14.7). В последних двух выражениях оператор  рассматривается как вектор:

                                            ,

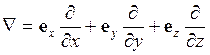а произведение  действует на каждую компоненту скорости.

Если мы переходим от полной производной к частной, объектом исследования становится не воздушная частица, а свойства воздуха в различных точках пространства, то есть, поля метеорологических величин (температуры, плотности, скорости и т.п.). Такой подход к изучению течений газов и жидкостей называется методом Эйлера, а независимые переменные x, y, z, t – переменными Эйлера. Здесь, как можно догадаться, вопрос о траектории отдельных воздушных частиц не ставится.

В методе Лагранжа все величины рассматриваются как функции времени и трёх параметров, выделяющих частицу из множества остальных. Например, тремя такими параметрами могут быть координаты частицы a,b,c в некоторый  момент времени t₀: . Тогда в методе Лагранжа мы находим значения физических величин частицы q(a, b, c, t) и ее координат x(a, b, c, t),  y(a, b, c, t),  z(a, b, c, t) в момент времени t. Изменяющиеся во времени координаты частицы определяют ее траекторию в пространстве, а зависимость от времени величины q определяет изменение содержания физической  величины в частице в ходе движения.

Переменные a, b, c, t называются переменными Лагранжа[6]. В методе Лагранжа мы следим за перемещением во времени и пространстве (за траекторией) каждой отдельной частицы среды и за изменением значений физических величин, характерных для этой частицы. Очевидно, такой подход полностью соответствует концепции движения материальной точки в классической механике. Разница в том, что таких точек в случае сплошной среды очень много, и нам нужно проследить движение каждой из них. Для этого кроме времени нам  необходимы переменные a, b, c, помечающие каждую частицу.

Естественно ожидать, что оба подхода к изучению движения сплошной среды должны быть эквивалентными,  и должны существовать способы перехода от одних переменных к другим. В частности, разрешив функциональные зависимости x=x(a,b,c,t),  y=y(a,b,c,t),  z=z(a,b,c,t) относительно переменных a,b,c, получим  a=a(x,y,z,t), b=b(x,y,z,t), c=c(x,y,z,t), то есть, перейдем к переменным Эйлера. При фиксированных значениях x,y,z  эти зависимости позволяют определить те точки среды (частицы жидкости), которые в момент времени t  приходят в данную точку пространства. Если физическая величина задана с точки зрения Лангранжа как функция q(a,b,c,t), то приведенные соотношения позволяют выразить зависимость этой величины от переменных Эйлера.

Рассмотрим теперь обратный переход от описания движения жидкости в рамках формализма Эйлера к описанию по Лагранжу. Пусть задано поле скоростей жидкости u=u(x,y,z,t), v=v (x,y,z,t), w=w(x,y,z,t). Компоненты скорости являются производными от соответствующих координат по времени при постоянных значениях параметров a,b,c, идентифицирующих частицу. Поэтому соотношения

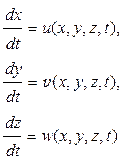
можно рассматривать как систему трех обыкновенных дифференциальных уравнений относительно x,y,z. Решив эту систему, определим x,y,z как функции времени и трех произвольных постоянных, определяемых по значениям x,y,z в некоторый момент времени t₀. Следовательно, эти постоянные идентифицируют частицу сплошной среды и являются переменными Лагранжа. Таким образом мы определяем зависимость координат частицы жидкости от времени и от идентифицирующих ее параметров, то есть, переходим к переменным Лагранжа. Подстановка найденных решений системы уравнений в выражения для полей физических величин q(x,y,z,t) преобразует их в выражения для физических величин индивидуальных частиц жидкости, то есть, осуществляет переход к переменным Лагранжа.