Статистические методы обработки данных в экологии: Методические рекомендации по изучению дисциплины, страница 7

4.2 Основные теоретические сведения

Цель и задачи дисперсионного анализа

При проведении исследований часто возникает необходимость оценки влияния на исследуемую величину одного или нескольких факторов, которые носят качественный характер. Примером может служить определение эффективности лечения несколькими лекарствами (первый фактор) при различных стадиях болезни (второй фактор). Подобные задачи решаются с использованием методов дисперсионного анализа (когда закон распределения исследуемой величины известен) или непараметрических методов (при неизвестном законе распределения).

Однофакторный дисперсионный анализ в модели с фиксированными эффектами

Пусть изучается влияние на исследуемую величину какого-либо одного фактора A, который имеет k уровней A₁ ,.., A_k, причем эти уровни зафиксированы экспериментатором в том смысле, что на исследуемую величину оказывают влияние именно уровни фактора, а все изменения за счет остальных (мешающих) факторов незначительны. В этом случае говорят о модели дисперсионного анализа с фиксированными эффектами.

Результаты измерений, когда на каждом из k уровней было проведено по n наблюдений исследуемой величины, можно представить в виде таблицы.

Модель такого анализа имеет вид

,   ,     .

где  – математическое ожидание (среднее), соответствующее j-му уровню фактора;  – генеральное среднее;  – дифференциальный эффект
j-го уровня фактора;  – независимые случайные величины, имеющие нормальное распределение с нулевым средним и одинаковой дисперсией σ².

Задача дисперсионного анализа – выяснение существенности влияния фактора A на исследуемую величину, т.е. определения отличия средних значений для каждой группы данных. Для этого необходимо проверить нулевую гипотезу H₀:  против альтернативной H₁: .

Проверка гипотезы H₀ основана на сопоставлении двух независимых оценок дисперсии σ². Одна из оценок действует вне зависимости от того, верна ли гипотеза H₀, вторая – существенно зависит от справедливости гипотезы H₀. Сопоставляя эти две оценки, можно вынести заключение о справедливости гипотезы H₀.

Указанные оценки строятся на основании разложения суммы квадратов отклонений значений x_ij от оценки генерального среднего

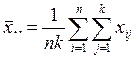
на две суммы квадратов:

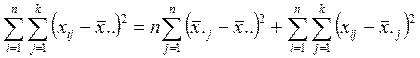
где 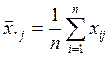 – выборочное среднее значение для j-го уровня фактора A.

Разделив указанные суммы на соответствующие им степени свободы, получим две оценки дисперсии σ²:

,       .

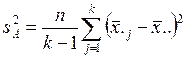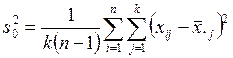Эти оценки при справедливости гипотезы H₀ являются несмещенными оценками дисперсии σ².

Однако, при отклонении от гипотезы H₀ оценка  получает смещение, величина которого тем больше, чем больше отклонение от гипотезы.

Сопоставление этих двух оценок дисперсии  и  осуществляется с использованием статистики Фишера

,

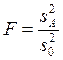которая имеет число степеней свободы k-1 и k(n-1).

Влияние фактора A на исследуемую величину считается значимым с уровнем значимости α, если вычисленное значение статистики F больше
α-процентной точки распределения статистики Фишера .

Если гипотеза о равенстве средних отвергнута, то можно сделать вывод о том, что все или некоторые средние μ_j не совпадают. Чтобы проверить, какие именно из средних не равны, нужно провести дополнительные исследования.

Можно, например, проверять несовпадение попарно, однако при этом общий уровень значимости (т.е. уровень значимости всех критериев) обычно будет отличаться от заданного уровня α. Поэтому следует применять методы множественного сравнения, позволяющие проверять также гипотезы для любых линейных комбинаций средних.

В методе множественных сравнений Шеффе для проверки гипотезы
H₀:  против H₁:  нужно построить доверительный интервал

,

где

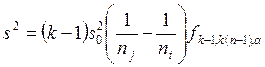
Если этот интервал не содержит ноль, то гипотеза H₀ отклоняется.