кафедра 304
Домашнее задание
по предмету «Численные методы»
Выполнила студентка 325 гр.
Старцева А. В.
Проверила ст. преподаватель каф. 304
Яровая О. В.
______________________
NUMERICAL INTEGRATION
Theoretical information
Integral of the
form ![]() in many cases it is impossible to find.
For example:
in many cases it is impossible to find.
For example:
· function can not be integrated
· function is given by the table
· function is given by a graph
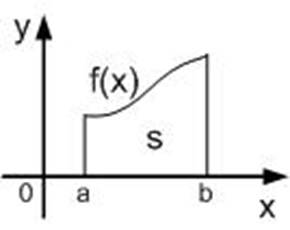
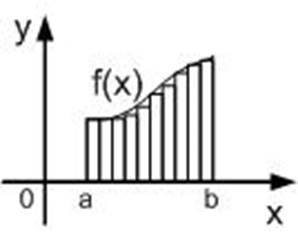
Definite
integral ![]() numerically equal to the area of the
figure bounded by the x-axis, direct x = a and x = b and the graph of the
function f (x).
numerically equal to the area of the
figure bounded by the x-axis, direct x = a and x = b and the graph of the
function f (x).
f(a)=y0
f(b)=y1 h=![]()
![]()
 n- predetermined
number of divisions
n- predetermined
number of divisions
Drawing 1.1 - Geometric interpretation of the definition Definite integral
Numerical
integration is a primary tool used by engineers and scientists to obtain
approximate answers for definite integrals that cannot be solved analytically.
We approach the subject of numerical integration. The goal is to
approximate the definite integral of f(x) over the interval [a, b] by
evaluating f(x) at a finite number of sample points.
Newton-Cotes methods are based on polynomial approximation of the
integrand.
In the process of numerical integration is necessary to calculate the
approximate value of the integral and estimate the error, regardless of the
method chosen.
Error will decrease with an increasing number of partitions of n of
the integration interval [a, b], due
to more accurate approximation of the integrand, but it will increase accuracy
by summing partial integrals, and the last error with some value n0
becomes dominant.
Numerical integration formulas dimensional case called quadrature.
The idea of building the quadrature formula is to replace the integrand polynomial chosen degree. We obtain the form of a quadrature formula, depending on the degree of the polynomial.
1. Replacement of a polynomial of degree zero
1) the method left rectangles
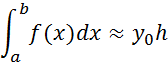
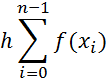
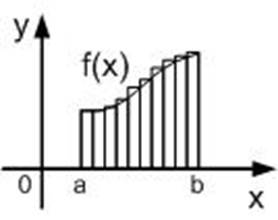
Drawing 1.2 - Geometric interpretation of the method left rectangles
2) the method right rectangles
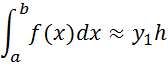
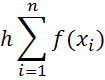
Drawing 1.3 - Geometric interpretation of the method right rectangles
3) the method of average rectangles
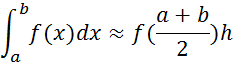
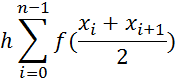
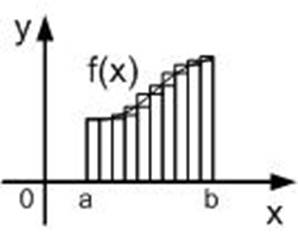
Drawing 1.4 - Geometric interpretation of the method of average rectangles
2. Replacement
of first-degree polynomial
the trapezoidal rule
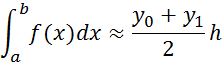
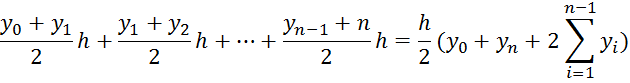
Drawing 1.4 - Geometric interpretation of the trapezoidal rule
3. Replacement
of a second degree polynomial
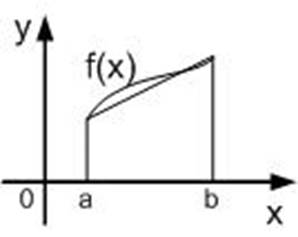
the Simpson's method
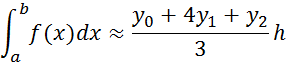
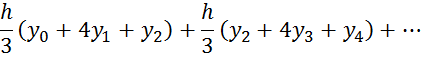
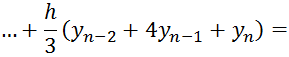
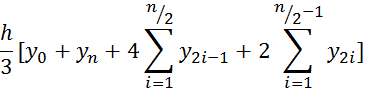
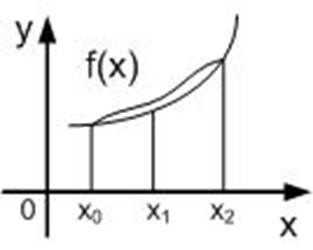
Drawing 1.5 - Geometric interpretation of the Simpson's method
Unit interval is 2h; n=2m
The formula works for an even number of intervals and odd number of points.
Formula Newton-Cotes
![]() ≈
≈ ![]()

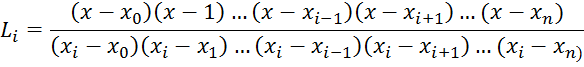
polynomial for constant grid
![]() ,
, ![]() ,
, ![]()
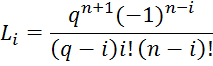
n- degree of the polynomial; i- number approximating polynomial
General view of the quadrature formula
![]() =
= ![]()
explicit form for the weighted
quadrature coefficients ![]()
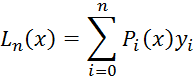
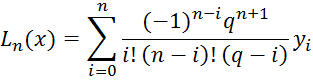
Lagrange polynomial for the uniform grid
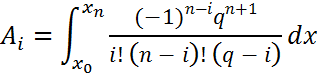
![]() ,
, 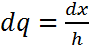
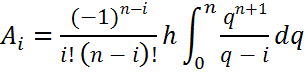
![]() ,
, ![]() – coefficients
Cotes i=(0,..n)
– coefficients
Cotes i=(0,..n)
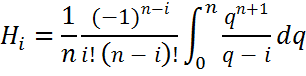
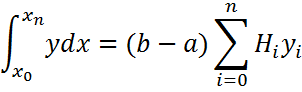
 ,
, ![]() , i=(0,..,n)
, i=(0,..,n)
Priori error
the methods left and right rectangles
![]()
the method of average rectangles
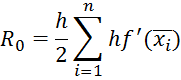
the trapezoidal rule
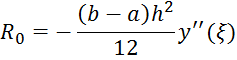
the Simpson's method
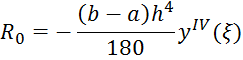
ξ є [a; b]
power h determines the order of the method
Posteriori error
General
view ![]()
p-order method
A - coefficient depending on the value of the derivative and integration method
The first formula Runge
w - the exact value, which should come numerical method
![]() - results of
numerical calculations
- results of
numerical calculations
w
= ![]() +
+![]() +O(
+O(![]() )
)
calculate increments kh, k – constant, which k>1 or k<1. A- remains unchanged, because we do not change the method. Necessary to carry out a priori error, that order of the method to determine.
w = ![]() +
+![]() +O((k
+O((k![]() ), equate:
), equate:
![]() +
+![]() =
=![]() +
+![]()
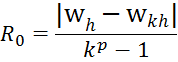
h, 2h 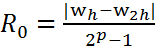
p=1 the methods left and right rectangles
![]()
p=2 the method of average rectangles, the trapezoidal rule
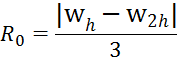
p=4 the Simpson's method
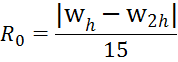
Calculate in Mathcad
|
|
|
|
|
|
|
|
Input
Tabulation of functions on a given interval [a,b]
|
|
|
|
|
|
|
|
|
|
|
|
Calculation of the definite integral using the built-in
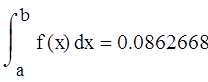
Program block that implements the calculation of the approximate value of the definite integral.
the Simpson's method
the trapezoidal rule
the method of average rectangles
the method right rectangles
the method left rectangles
|
|
|
|
|
|
|
|
|
|
Calculating a posteriori error computation
|
|
|
|
Calculating a priori calculation errors
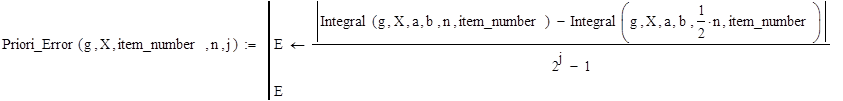
|
|
|
|
|
|
|
|
|
|
Calculate in Matlab
function res = Integral(func, str, a , b, n);
%str - methods name, a,b - distance, n - number of points
h = (b-a)/n;
Sum = 0;
switch (str)
case 'Simpson'
q1=0; q2=0;
for i = 1:n-1
if (mod(i,2)==1) q1 = q1+myfunc(func,a + i*h);
else q2 = q2+myfunc(func,a + i*h);
end;
end;
Sum = (h/3)*( myfunc(func,a) + 4*q1 + 2*q2 + myfunc(func,b) );
case 'Trapezium'
for i = 1:n-1
Sum = Sum + myfunc(func,a + i*h);
end;
Sum = (h/2)*( myfunc(func,a) + 2*Sum + myfunc(func,b) );
case 'LeftRectangles'
for i=1:n-1
Sum = Sum + h*myfunc(func,a + i*h);
end;
Sum = h*myfunc(func,a) + Sum;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.