Формула Тейлора для многочлена

Лекция 10

Формула Тейлора для многочлена. Если есть целый много­член степени п:

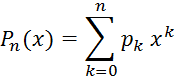
то, последовательно дифференцируя его и раз:

и полагая во всех этих формулах х = 0, найдем выражения коэффициентов многочлена через значения самого многочлена  и  его  производных  при 

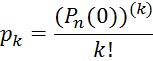
Подставим эти значения коэффициентов в многочлен:

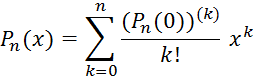
Эта формула отличается от исходной записью коэффициентов.

Вместо того чтобы разлагать многочлен по степеням , можно было бы взять его разложение по степеням , где есть некото­рое постоянное частное значение х:

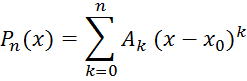
Полагая   ,  для  коэффициентов много­члена

имеем, по доказанному, выражения:

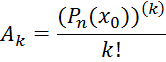
т. е.  коэффициенты разложения оказались вы­раженными через значения самого многочлена и его производных при  х = х₀.

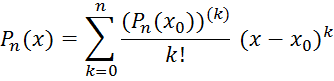
Это формула, так же как и ее частный (при х₀ = 0) случай, назы­вается формулой Тейлора (В. Taylor). Известно, какие важ­ные применения она имеет в алгебре.

Обратимся теперь к рассмотрению произвольной функции  , вообще не являющейся целым многочленом. Предполо­жим, что для нее в некоторой точке х₀ существуют производные всех порядков до л-го включительно. Это значит, точнее говоря, что функ­ция определена и имеет производные всех порядков до (n- 1)-го вклю­чительно в некотором промежутке , содержащем точку х₀, и, кроме того, имеет производную n-го порядка в самой точке х₀. Тогда для функции  может быть составлен много­член

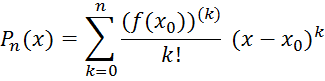
Согласно предшествующему замечанию, этот многочлен и его производные (до n-й включительно) в точке х₀ имеют те же значения, что и функция и ее производ­ные.

Но на этот раз, если только  не есть целый многочлен n-й степени, уже нельзя утверждать равенства . Многочлен дает лишь некоторое приближение функции . Поэтому особый интерес приобретает изучение разности

Установим, прежде всего, что при  эта разность представ­ляет собой бесконечно малую порядка выше п-го (по сравнению с ):

По свойству многочлена для функции , очевидно, будут иметь место равенства

Мы сейчас установим общее утверждение: если для какой-либо функции , имеющей в точке х₀ производные до п-го по­рядка включительно, выполняются условия

,

 то имеет место соот­ношение

 Доказательство проведем по методу математической индукции. При

 п = 1  это утверждение имеет вид:

если функция г(х), имеющая в точке х₀ производную (первого порядка), удовлетворяет условиям

,

то                             

Его справедливость проверяется непосредственно:

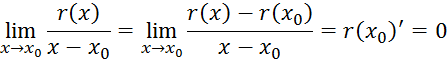
Предположим теперь, что сформулированное выше утвер­ждение справедливо для какого-либо , и докажем, что оно остается верным и при замене п  на п + 1, т. е. что: если для какой –либо функции , имеющей в точке х₀ производные до (п - 1)-го порядка включительно, выполняются условия

то

Проверим  непосредственно:

Таки образом                что и требовалось доказать.

Таким образом, наше утверждение оправдано для любого нату­рального п,. Тогда для представления функции мы получаем формулу

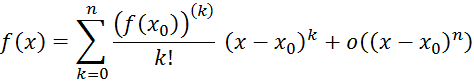
которая от формулы для многочлена разнится наличием допол­нительного члена. В указанной форме дополнительный член был дан Пеано (G. Реапо). Полученная формула и называется фор­мулой Тейлора сдополнительным членом в форме Пеано.

Всего проще выглядит формула Тейлор а, если

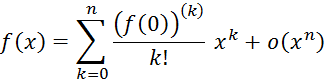
Эту  формулу связывают с именем Маклорена.

К этому частному случаю всегда можно свести дело, взяв за новую независимую переменную.

Рассмотрим в виде примера некоторые конкретные разложения по этой формуле для элементарных функций.

1)  Пусть ; тогда при любом (k=1, 2, 3, ... ). Так как в этом случае  при любом (k=1, 2, 3, ... )  тогда разложение функции в ряд Маклорена, запишется

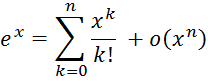
2) Разложим в ряд Маклорена   . Несложно показать, что

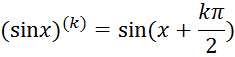
Найдем производную в нуле

Если , то

Положив , получаем

тогда разложение функции в ряд Маклорена, запишется

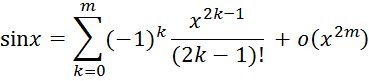
3)  Разложим в ряд Маклорена   . Аналогично предыдущему примеру

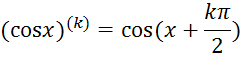
Найдем производную в нуле

Если , то

Положив , получаем

тогда разложение функции в ряд Маклорена, запишется

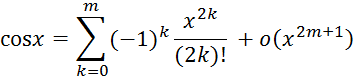
4)  Рассмотрим теперь логарифмическую функцию ,

Найдем производную в нуле

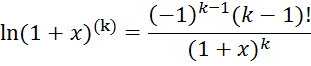
Подставляя , получим

и разложение функции в ряд Маклорена, запишется

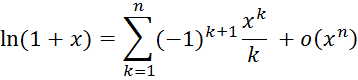
Разложения, полученные в примерах 1-4, часто встречаются в приложениях, поэтому выпишем их еще раз.

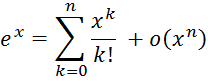
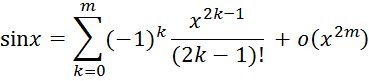
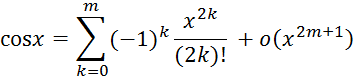
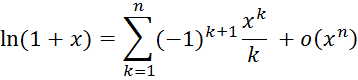
Выясним теперь, как по произ­водной функции можно судить о возрастании (убывании) самой функ­ции в данном промежутке. Остановимся сначала на случае функции, монотонно возрастающей в широком смысле, т. е. не убы­вающей (или монотонно убывающей в широком с м ы с л е, т. е. не возрастающей).

Теорема 2. Пусть функция  определена и непрерывна в про­межутке X и внутри него имеет конечную производную. Для того чтобы  была в X монотонно возрастающей (убывающей) в широком смысле, необходимо и достаточно условие  внутри промежутка.

Необходимость. Если монотонно возрастает, хотя бы в широком смысле, то, взяв