Если функция u = f(x,y,z),
зависящая от трех переменных, которые, в свою
очередь, зависят еще от переменных t и 
, т. е. 
и 
, тогда
,
.
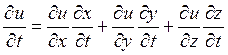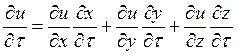Полный дифференциал первого порядка для функции многих переменных имеет вид
.
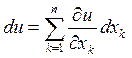Производные высших порядков вводятся индуктивно, т. е.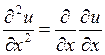 
и т.п.
Производные 
, 
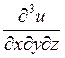и т.д. называются смешанными произвонымн.
Полный дифференциал n–го порядка вычисляется по формуле
.
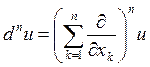Если взять некоторое
направление 
, то производная
от функции в этом направлении вычисляется следующим образом:
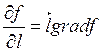, где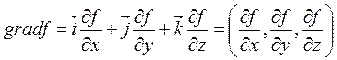 
Пример 3.1.1. Вычислить производную функции 
в точке М0(1,1) в направлении
вектора 
.
Решение. По определению 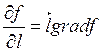найдем
в точке M0(1,l). Для
этого вычислим частные производные.
,
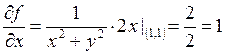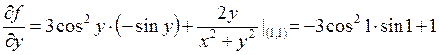
Из вектора сделаем единичный
вектор
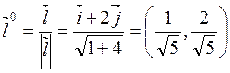
и окончательно получим:
.
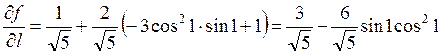Ответ: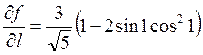 
.
Пример 3.1.2. Найти второй дифференциал функции z, которая задана неявно: х3у + yz + z3 = 3.
Решение. По определению
.
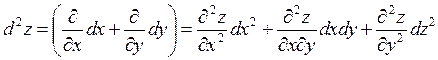От обеих частей функции, заданной
в неявном виде, возьмем производную по х: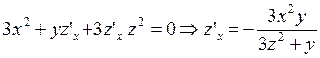 
, а затем еще раз производную по
x: 
.
Из этого равенства найдем 
:
.
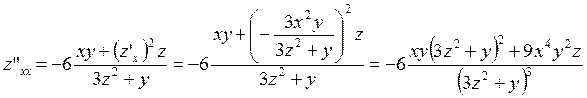Найдем смешанную производную
,. Равенство 
дифференцируем
по у:
;
.
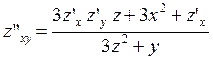От функции 
возьмем производную по
у: 
. затем еще раз по у.
Из равенств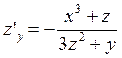 
; 
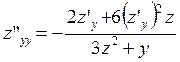получим
,
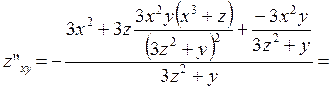
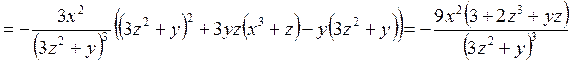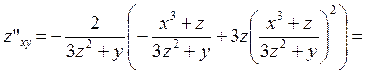
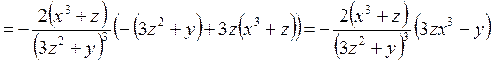
и окончательно запишем выражение для второго дифференциала
.
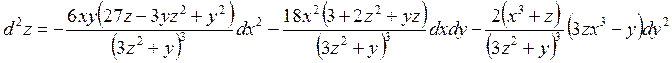Учебники: [16], [17].
Аудиторная работа: [3, №№ 3259, 3292].
Самостоятельная работа: [3, №№ 3260, 3293].
Точка М0
называется точкой локального максимума (минимума), если значение функции в этой
точке будет наибольшим (наименьшим) из окрестности точки М0.
Необходимое условие существования локального экстремума: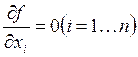 
, или 
.
Сформулируем достаточное условие для функции двух
переменных. Введем обозначения: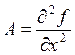 
; 
; 
.
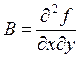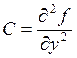Если D = AC – В2 > 0, то в точке М0 – локальный экстремум, причем, если А > 0 – локальный минимум, а если А < 0 – локальный максимум.
Для функций многих переменных, т. е. 3,4,…,n, достаточным условием будет условие знакопостоянства второго дифференциала.
Второй дифференциал представляет собой квадратичную форму, а условие знакопостоянства квадратичной формы дает критерий Сильвестра.
Если d2f > 0, то в точке М0 – локальный минимум, если d2f < 0 ‑ локальный максимум.
Функция u = f(р) имеет условный максимум (минимум) в точке Р0,
если существует такая окрестность точки Р0, для всех точек Р
которой 
, удовлетворяющих
уравнениям связи
выполняется неравенство 
.
Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа.
.
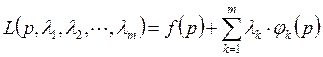Пример 3.2.1. Найти точки экстремума функции
.
Решение. Из необходимого условия экстремума найдем точки, подозрительные на экстремум:
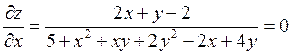
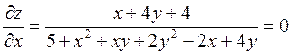
Отсюда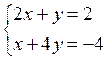 
,
, 
.
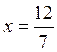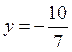Проверим для точки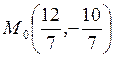 
, достаточное условие. Для этого
найдем вторые производные:
;
;
;
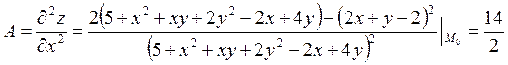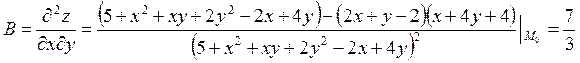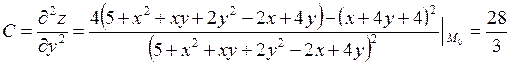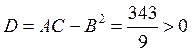
Экстремум есть и т. к. А > 0, то это — локальный минимум.
Ответ. В точке 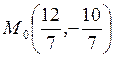локальный минимум 
.
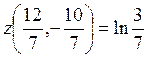Пример 3.2.2. Найти экстремум функции 
при условии
.
Решение. Для нахождения условного экстремума составим функцию Лагранжа:
.
Удовлетворим необходимому условию существования экстремума.
,
,
,
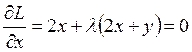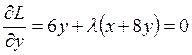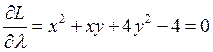Разрешая эту систему, получаем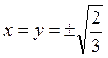 
; 
;
; 
.
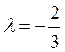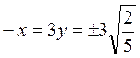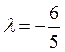Так как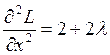 
; 
; 
,
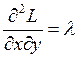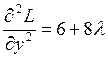то 
1. 
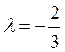
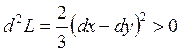— локальный
минимум;
2. 
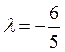
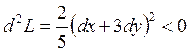— локальный
максимум.
Следовательно, в точках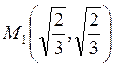 
, 
, 
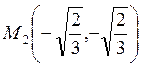— min,
а в точках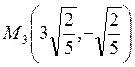 
, 
, 
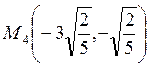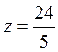локальный
максимум.
Учебники: [16], [17].
Аудиторная работа: [3, №№ 3412, 3416].
Самостоятельная работа: [3, №№ 3414, 3417].
Уравнение касательной плоскости, в случае явного задания поверхности, т. е. z = z(x,y) в точке М0(х0,у0) записывается
.
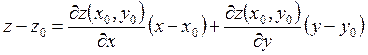Если поверхность задана в неявном виде F(x,y,z), то нормаль к касательной плоскости имеет вид
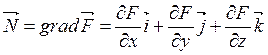
Прямая называется нормальной к поверхности в точке, если она проходит через эту точку и перпендикулярна к касательной плоскости, проходящей через эту же точку.
В случае явного задания поверхности нормальная прямая имеет вид
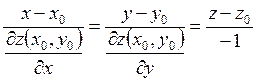
В случае неявного задания поверхности
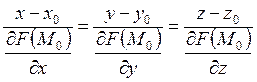
Пример 3.3.1. Написать уравнение касательной плоскости и нормальной прямой к поверхности х4у + 2х2у3 + xyz2 +ez =3 в точке M0(l,l,0).
Решение. Уравнение поверхности задано в неявном
виде F(x,y,z) = х4у + 2х2у3 + xyz2 + ez – 3 = 0. Найдем
нормаль к касательной плоскости: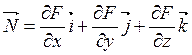 
.
Найдем частные производные от функции F в точке М0:
,
,
,
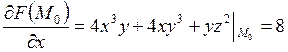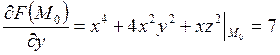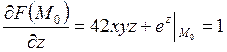тогда 
и
уравнение плоскости в точке М0 запишется
8(х – l) + 7(y – 1) + z = 0, или 8х + 7у + z = 15.
Уравнение нормальной прямой к поверхности в точке М0
.
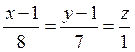1. Частные производные и полный дифференциал.
2. Производные от сложных функций.
3. Производные неявно заданных функций.
4. Касательная плоскость и нормаль к поверхности.
5. Геометрический смысл полного дифференциала.
6. Частные производные высших порядков.
7. Формула Тейлора для функции нескольких переменных.
8. Экстремум функции нескольких переменных.
9. Условный экстремум.
Учебники: [7, гл. 8], [9, гл. 6, 7], [16, гл. 13], [33, ч. 2, гл. 4, §§ 4.1-4.6].
Аудиторная работа: [3, №№ 1685, 1688, 1693, 1694, 1696, 1698, 1699, 1712, 1715, 1716, 1719, 1723, 1724, 1742, 1744, 1757, 1833, 1836, 1837, 1842, 1851, 1855, 1874, 1877, 1884, 2013, 2017, 2023, 2025, 2037, 2039, 2048, 2051, 2071, 2073, 2090, 2093, 2105, 2111, 2152, 2155], [7, гл. 8, №№ 5, 6, 7, 10, 12, 15, 16, 23, 27, 29, 33, 36, 40, 43, 51, 52, 56, 67, 71, 77, 78, 80, 90, 91, 92, 95, 102, 106, ПО, 113, 114, 118, 123, 124, 125, 147, 148, 153, 158, 162], [20, ч. 1, №№ 6.19, 6.23, 6.25, 6.27, 6.29, 6.43, 6.48, 6.65, 6.70, 6.79, 6.115, 6.117, 6.123, 6.125, 6.131, 6.133, 6.143, 6.153, 6.163, 6.172, 6.174, 6.191, 6.193, 6.195, 6.203, 6.219, 6.239, 6.245, 6.248, 6.253, 6.263], [33, №№ 34.1, 34.3, 34.5, 34.7, 34.9, 34.11, 35.1, 35.3, 35.5, 35.7, 35.9, 35.11, 36.1, 36.3, 36.5, 36.7, 36.9, 36.11, 37.1, 37.3, 37.5, 37.7, 37.9, 37.11, 38.1, 38.3, 38.5, 38.7, 38.9, 38.11, 39.1, 39.3, 39.5, 39.7, 39.9,39.11], [38, №№ 1.2.1 - 1.2.16,2.2.1 -2.2.16,3.2.1 -3.2.8,4.2.1 -4.2.12, 5.2.1-5.2.10].
Самостоятельная работа: [3, №№ 1686, 1689, 1690, 1695, 1697, 1700, 1713, 1717, 1720, 1725, 1726, 1737, 1745, 1768, 1834, 1838, 1841, 1853, 1860, 1876, 1881, 1885, 2012, 2016, 2027, 2028, 2038, 2041, 2050, 2069, 2074, 2091, 2095, 2110, 2112, 2153, 2154], [7, гл. 8, №№ 8, 11, 13, 14, 18, 20, 21, 25, 28, 30, 31, 34, 35, 41, 44, 45, 47, 53, 57, 61, 68, 69, 79, 81, 84, 87, 93, 94, 97, 99, 109, 112, 116, 119, 120, 121, 127, 146, 149, 150, 154, 159], [20, ч. 1, №№ 6.21, 6.26, 6.28, 6.40, 6.41, 6.56, 6.58, 6.64, 6.66, 6.72, 6.80, 6.116, 6.122, 6.124, 6.126, 6.130, 6.134, 6.136, 6.158, 6.168, 6.171, 6.175, 6.194, 6.196, 6.198, 6.202, 6.218, 6.240, 6.242, 6.246, 6.250, 6.256], [33, №№ 34.2, 34.4, 34.6, 34.8, 34.10, 34.12, 35.2, 35.4, 35.6, 35.8, 35.10, 35.12, 36.2, 36.4, 36.6, 36.8, 36.10, 36.12, 37.2, 37.4, 37.6, 37.8, 37.10, 37.12, 38.2, 38.4, 38.6, 38.8, 38.10, 38.12, 39.2, 39.4, 39.6, 39.8, 39.10, 39.12], [38, №№ 1.3.1 - 1.3.16, 2.3.1 - 2.3.16, 3.3.1 - 3.3.8, 4.3.1 - 4.3.12, 5.3.1-5.3.10].
Операция нахождения первообразной функции является обратной по отношению к операции дифференцирования функции. Поэтому перед изучением этой темы рекомендуется повторить таблицу производных элементарных функции и основные правила дифференцирования.
Определение. Пусть функция f(x) определена на интервале (a, b). Функция F(x) называется первообразной для функции f(x) на интервале (а, b), если F(x) определена и дифференцируема на интервале (а, b) и в каждой точке этого интервала F’(x) = f (x).
Таким образом, первообразная для f(x) — это такая функция, продифференцировав которую, получаем f(х).
Пример 4.1.1. Первообразной для функции f(x) = sinx на интервале 
является функция F(x) = – cos x, т.к.
F'(x) = (–cos x)' = sin x = f(x).
Пример 4.1.2. Первообразной для функции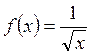 
на интервале 
является функция 
, т.к.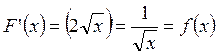 
.
При работе с первообразной интервал (a, b) обычно опускается.
Из определения первообразной следует, что если F(x) является первообразной для функции f(х), то F(x) + С при любой постоянной С также
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
